How to solve $B = x^c - (1 - x)^c$
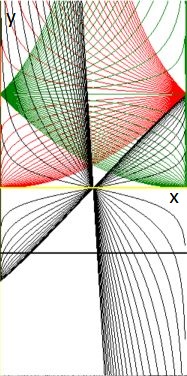
A picture says more than a thousand words. Below is a sketch of the curves
$\;\color{red}{y=x^c}$ , the curves $\;\color{green}{y=(1-x)^c}\;$ and their difference
$\;y=x^c - y=(1-x)^c$ . The symmetries are clearly seen.
The range of $\,c\,$ has been chosen as $\;-2 < c < +2\;$ with steps of $1/10$ .
For $\;c < 0$ , the curves $\;\color{red}{y=x^c}\;$ as well as the curves $\;\color{green}{y=(1-x)^c}\;$
are above the line $\,y=1$ , for $\;c > 0\;$ they
are below that line and $\;0 \le y \le 1$ . A sample line $\;y=B\;$ is drawn for
$\;B=-0.7$ . The intersects with the black curves are solutions. I see no other way
than numerically solve these equations, given some definite values of $\,B\,$ and $\,c$ .
The picture might help then to find initial iterates.