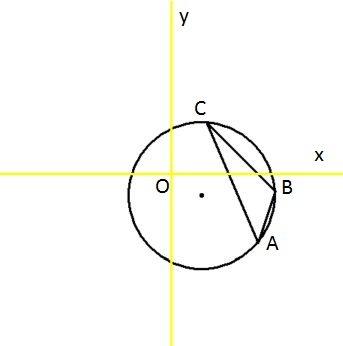
Find equation for circle related to a triangle
Substitute $(A,B,C)$ into $(x-a)^2 + (y-b)^2 = R^2$ :
$$
(5-a)^2 + (-4-b)^2 = R^2 \\
(6-a)^2 + (-1-b)^2 = R^2 \\
(2-a)^2 + (3-b)^2 = R^2
$$ $$
a^2 - 10 a + 25 + b^2 + 8 b + 16 = R^2 \\
a^2 - 12 a + 36 + b^2 + 2 b + 1 = R^2 \\
a^2 - 4 a + 4 + b^2 - 6 b + 9 = R^2
$$
Subtract the second equation from the first one and the third equation from the second one:
$$
2 a - 11 + 6 b + 15 = 0 \\
- 8 a + 32 + 6 b - 3 = 0
$$ $$
2 a + 6 b = - 4 \\
- 8 a + 8 b = - 24
$$
Add the second equation to $4 \times$ the first one .. and do the rest:
$$
32 b = - 40 \quad \Longrightarrow \quad b = - 5/4 \\
2\cdot 2 a = - 8 + 15 = 7 \quad \Longrightarrow \quad a = 7/4 \\
R^2 = (2-a)^2 + (3-b)^2 = 145/8
$$
So the circle is:
$$
(x-7/4)^2 + (y+5/4)^2 = \left(\sqrt{145/8}\right)^2
$$
Still don't know what you mean by "district" ..
