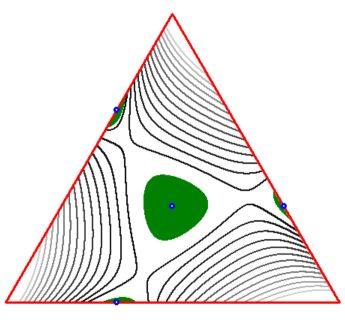
Define the function to be investigated as: $$ F(a,b,c) = \sqrt{24a^2b+25}+\sqrt{24b^2c+25}+\sqrt{24c^2a+25} - 21 $$ Scanning the inside of the triangle (picture on the left) pixel by pixel (i.e. numerically) reveals that:
minimum = -5.97874499595267E+0000 ; maximum = -1.86093567294196E-0005The exact minimum is at the vertices of the triangle: $F(3,0,0)=F(0,3,0)=F(0,0,3)=-6$ , just beyond reach of the numerics.
for g := 1 to 16 do
begin
level := -sqr(g/8); { level = minus g/8 squared }
More black means closer to the maximum. Of course we already know that:
$$
F(1,1,1) = 0 \; ; \; F(2,1,0) = 0 \; ; \; F(0,2,1) = 0 \; ; \; F(1,0,2) = 0
$$
These places are indicated as $\color{blue}{blue}$ spots in the picture on the right.
So there is strong evidence (ipse est NO "rigorous proof") that $0$ is indeed the maximum. My 2 cents worth ..
EDITs. Picture on the right augmented with $\color{green}{green}$ areas where $|F(a,b,c)| < 0.1$ .
If $F(a,b,c)$ is specified for an edge of the equilateral triangle, then we can do some analytical work,
though it remains a modest attempt:
$$
f(x) = F(3-x,x,0) = \sqrt{24(3-x)^2x+25}-11
$$
Derivative zero:
$$
f'(x) = \frac{1}{2}24\frac{-2(3-x)x+(3-x)^2}{\sqrt{24(3-x)^2x+25}} = 0
\quad \Longleftrightarrow \quad x\in\{3,1\}
$$
Giving the known minimum $F(0,3,0)$ and the known maximum $F(2,1,0)$ ,
the only difference being that these are now proven unique, at the triangle's edges.
In order to demonstrate that the problem is "not so easy", let's specify again,
for a line through one vertex of the triangle $(3,0,0)$ and the midpoint $(1,1,1)$:
$$
g(x) = F(3-2x,x,x) = \sqrt{24(3-2x)^2x+25}+\sqrt{24x^3+25}+\sqrt{x^2(3-2x)+25}-21
$$
Then we already know that a solution of $g'(x)=0$ is given by $F(1,1,1)=0$.
But, if this is fed into MAPLE ,
then all I've got is a seemingly endless loop:
> solve(diff(g(x),x)=0,x); Warning, computation interrupted