The Matlab code may be explained by the fact that the curvature is one divided by the radius of an
Osculating circle .
Since all what you have is a bunch of data points, it has to be decided which data points
may be relevant for the curvature at some place at the curve. At least three of them are needed to determine a circle.
If more data points are taken, then a least squares procedure will be needed in order to determine a Best Fit Circle to them.
For a better understanding of the latter, one might read the following document:
There is no unambiguous recipe for how many data points to take for an osculating circle at some place at the curve.
It all depends upon your data and all you can have is a decent approximation. Now I don't know how Matlab works,
but it seems to me that these data points form the arrays $x$ and $y$ in the code. However, speaking for myself,
I'd rather ignore this particular implementation and start from scratch, with my own understanding of the matter.
Update. To demonstrate that Robert Israel's
method (as explained in the reference) does indeed work:
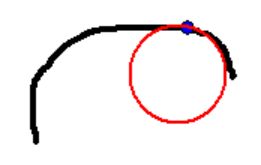
The code itself is to large to fit into the margin. Serious: it really has no sense to publish all those (Delphi Pascal)
programming details: I'm pretty sure that wouldn't add much to understanding.
But if someone asks me for the source code, then he or she can have it for free.
