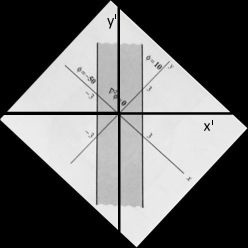
Look at it in this way. Rotate the picture $45^o$ clockwise around the origin:
$$
x' = (x+y)/\sqrt{2} \quad ; \quad y' = (x-y)/\sqrt{2}
$$
(Where one might ask why the Laplace equation is invariant for rotations)
Then the Laplace problem becomes essentially one-dimensional.
And the boundaries conditions become respectively:
$$
x' = (x+y)/\sqrt{2} = \pm 3/\sqrt{2}
$$
The equation itself is, in the new $(x',y')$ coordinates:
$$
\frac{d^2\phi}{d(x')^2} = 0 \quad \Longrightarrow \quad \phi(x',y') = C x' + D
$$
That is: linear. With boundary conditions:
$$
\phi(-3/\sqrt{2}) = -50 \quad ; \quad \phi(+3/\sqrt{2}) = +10
$$
Consequently:
$$
-50 = C(-3/\sqrt{2}) + D \quad ; \quad +10 = C(+3/\sqrt{2}) + D
$$
When solving for $C$ and $D$:
$$
60 = C\, 6/\sqrt{2} \quad \Longrightarrow \quad C = 10\sqrt{2}
\quad \Longrightarrow \quad D = -20
$$
Now rotate the solution back $45^o$ counterclockwise, giving:
$$
\phi(x,y) = 10\sqrt{2}(x+y)/\sqrt{2} - 20 = 10(x+y) - 20
$$
Which is the desired solution.
One can think of a shortcut, once you've got the idea.
Linearity:
$$
\phi(x+y) = (x+y)A+B
$$
Boundary conditions:
$$
\phi(x+y=-3) = -50 \quad ; \quad \phi(x+y=+3) = +10
$$
Giving:
$$
\left. \begin{matrix} -3A+B = -50 \\ +3A+B = +10 \end{matrix} \right\}
\quad \Longrightarrow \quad \left\{ \begin{matrix} A = 10 \\ B = -20 \end{matrix} \right.
$$
LATE EDIT. Proof that the Laplace operator is invariant for rotations in the plane.
$$
x_1 = \cos(\theta)\,x - \sin(\theta)\,y \\
y_1 = \sin(\theta)\,x + \cos(\theta)\,y
$$
Chain rules:
$$
\frac{\partial}{\partial x} = \frac{\partial x_1}{\partial x}\frac{\partial}{\partial x_1}
+ \frac{\partial y_1}{\partial x}\frac{\partial}{\partial y_1} =
\cos(\theta)\frac{\partial}{\partial x_1}+\sin(\theta)\frac{\partial}{\partial y_1} \\
\frac{\partial}{\partial y} = \frac{\partial x_1}{\partial y}\frac{\partial}{\partial x_1}
+ \frac{\partial y_1}{\partial y}\frac{\partial}{\partial y_1} =
-\sin(\theta)\frac{\partial}{\partial x_1}+\cos(\theta)\frac{\partial}{\partial y_1}
$$
Take squares:
$$
\frac{\partial^2}{\partial x^2} =
\left[\cos(\theta)\frac{\partial}{\partial x_1}+\sin(\theta)\frac{\partial}{\partial y_1}\right]^2
= \cos^2(\theta)\frac{\partial^2}{\partial x_1^2}
+2\cos(\theta)\sin(\theta)\frac{\partial^2}{\partial x_1 \partial y_1}+
\sin^2(\theta)\frac{\partial^2}{\partial y_1^2} \\
\frac{\partial^2}{\partial y^2} =
\left[-\sin(\theta)\frac{\partial}{\partial x_1}+\cos(\theta)\frac{\partial}{\partial y_1}\right]^2
= \sin^2(\theta)\frac{\partial^2}{\partial x_1^2}
-2\cos(\theta)\sin(\theta)\frac{\partial^2}{\partial x_1 \partial y_1}+
\cos^2(\theta)\frac{\partial^2}{\partial y_1^2}
$$
Add together:
$$
\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} =
\frac{\partial^2}{\partial x_1^2} + \frac{\partial^2}{\partial y_1^2}
$$