The following is a related issue @ Mathematics Stack Exchange:
And the main keyword is found @ Wikipedia as: Using that theory we have for $-\pi/4<\operatorname{arg}(z)<\pi/2$ , at $z=0$ : $$ \frac{dz}{dw} = K'(w-0)^{(\pi/2+\pi/4)/\pi-1} = K' w^{-1/4} \quad \Longrightarrow \quad z = K w^{3/4} + C $$ With $K = 4/3\cdot K'$. Substitute $z=0$ and $w=0$ herein and find that $C=0$. Next step: $$ i = K(-1)^{3/4} = K e^{i\,3\pi/4} = K/\sqrt{2}(-1+i) \quad \Longrightarrow \quad K = \frac{1-i}{\sqrt{2}} $$ It follows that: $$ w(z) = \left(\frac{\sqrt{2}\,z}{1-i}\right)^{4/3} = \left(e^{i\pi/4} z\right)^{4/3} = g(z) $$ Consequently: $$ w(1-i) = \left(\sqrt{2}\right)^{4/3} = 2^{2/3} \ne 2 $$ This is not consistent with the OP's question and it explains the above disclaimer.
Update. It seems that my wrong answer has served as an Ansatz
for the correct answer by Christian Blatter: $\,w(z) = T(g(z))$ ;
so it has served a purpose and I'm not going to delete it.
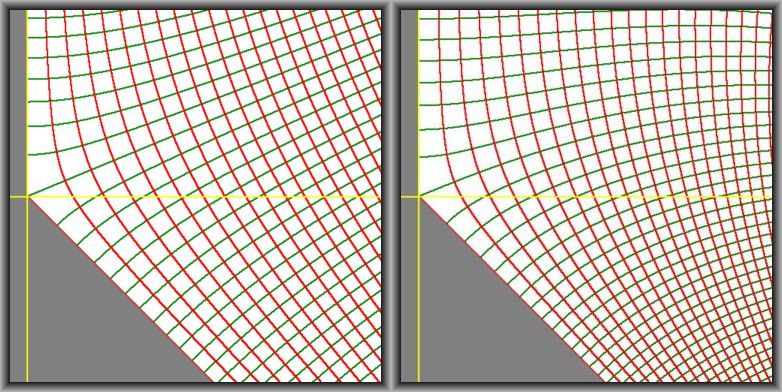
A contour plot of both $\,g(z)\,$ - on the left - and $\,T(g(z))\,$ - on the
right - shows the differences.
The viewports are $\,-0.1 < x < 1.9$ ,
$-1 < y < +1\,$ with $\,z = x+i\,y$ ; isolines of the Imaginary parts
are in $\color{red}{red}$ and isolines of the Real parts are in
$\color{green}{green}$ . Contour levels are between $-4$ and $+4$
with steps of $4/30$.
