Disclaimer. This is not an answer, but rather a too long comment with some graphics in it.
The equation looks like the common ODE for a harmonic oscillator: $y'' + \omega^2 y = 0$
with the square of the frequency varying proportional to "time" $x$ .
Numerical simulation with the initial conditions $y(0)=0$ and $y'(0)=1$ reveals that the solution
indeed looks like that (I hate solutions without a picture, you know):
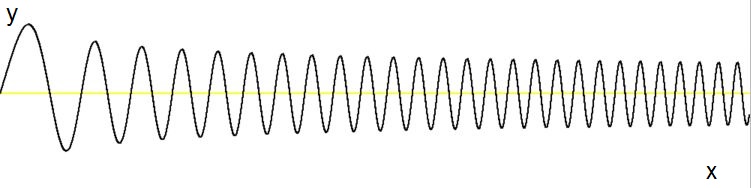
The viewport is $\,0 < x < 40\,$ and $\,-1.5 < y < +1.5\,$.
Program (Delphi Pascal) snippet for doing the calculations and the drawing (not optimized at all):
{
The equations of motion are solved numerically as follows.
Start with: y(0) = 0 ; x = 0 ;
(y(dx) - y(0))/dx = v ==> y(dx) = y(0) + v.dx
y(x + dx) - 2.y(x) + y(x - dx)
------------------------------ + x.y(x) = 0 ==>
dx^2
y(x + dx) = 2.y(x) - y(x - dx) - dx^2.x.y(x) ==>
y(0.dx) = 0
y(1.dx) = y(0.dx) + v.dx
y(2.dx) = 2.y(1.dx) - y(0.dx) - dx^2.x.y(1.dx)
y(3.dx) = 2.y(2.dx) - y(1.dx) - dx^2.x.y(2.dx)
..............................................
y(k+1).dx) = 2.y(k.dx) - y((k-1).dx) - dx^2.x.y(k.dx)
}
procedure bereken;
const
N : integer = 40000;
v : double = 1;
var
x,dx,y0,y1,y2 : double;
k : integer;
begin
x := 0; dx := 0.001;
y0 := 0; y1 := y0+v\*dx;
Form1.Image1.Canvas.MoveTo(x2i(0),y2j(0));
for k := 0 to N-1 do
begin
x := x + dx;
y2 := 2\*y1 - y0 - dx\*dx\*x\*y1;
Form1.Image1.Canvas.LineTo(x2i(x),y2j(y2));
y0 := y1; y1 := y2;
end;
end;
Note that the solution becomes very oscillatory (i.e. singular) for $x\to\infty$ .
However, the frequency only varies with the square root of the distance: $\omega=\sqrt{x}$ ,
therefore it doesn't happen immediately.
