Is there an established method for assigning a truth value $0<t<1$ to undecidable statements?

Fuzzyfied Logic

Let $\,x,y,z\,$ be sets (set theory) or propositions (mathematical logic). For these elements, the axioms of boolean algebra are supposed to be valid: $$ \begin{array}{lll} z \cap z = z & ; & z \cup z = z \\ y \cap z = z \cap y & ; & y \cup z = z \cup y \\ x \cap (y \cap z) = (x \cap y) \cap z & ; & x \cup (y \cup z) = (x \cup y) \cup z \\ x \cap (y \cup z) = (x \cap y) \cup (x \cap z) & ; & x \cup (y \cap z) = (x \cup y) \cap (x \cup z) \\ 0 \cap z = 0 & ; & 1 \cup z = 1 \\ 1 \cap z = z & ; & 0 \cup z = z \\ \overline{y \cap z} = \overline{y} \cup \overline{z} & ; & \overline{y \cup z} = \overline{y} \cap \overline{z} \\ z \cap \overline{z} = 0 & ; & z \cup \overline{z} = 1 \\ \overline{\overline{z}} = z & & \end{array} $$ Let the above axioms are valid for numbers $x,y,z$ which assume values from the set $\,\{0,1\}$ . We seek a generalization of the axioms for numbers which assume values between $0$ and $1$ , that is from the interval $\,\left[0,1\right]$ . Define for $0\le a\le 1$ and $0\le b\le 1$ : $$ \begin{array}{lllll} a \cap b := a.b & ; & a \cup b := a + b - a.b & ; & \overline{a} := 1 - a \end{array} $$ Elementary number algebra reveals that the following axioms are still valid: $$ \begin{array}{lll} y \cap z = z \cap y & ; & y \cup z = z \cup y \\ x \cap (y \cap z) = (x \cap y) \cap z & ; & x \cup (y \cup z) = (x \cup y) \cup z \\ 0 \cap z = 0 & ; & 1 \cup z = 1 \\ 1 \cap z = z & ; & 0 \cup z = z \\ \overline{y \cap z} = \overline{y} \cup \overline{z} & ; & \overline{y \cup z} = \overline{y} \cap \overline{z} \\ \overline{\overline{z}} = z & & \end{array} $$ But other axioms are no longer valid: $$ \begin{array}{lll} z \cap z \ne z & ; & z \cup z \ne z \\ x \cap (y \cup z) \ne (x \cap y) \cup (x \cap z) & ; & x \cup (y \cap z) \ne (x \cup y) \cap (x \cup z) \\ z \cap \overline{z} \ne 0 & ; & z \cup \overline{z} \ne 1 \end{array} $$

Fuzzy Equality

The following truth table (: logic) and Karnaugh diagram (: set theory) are valid for equivalent (read: equal) boolean elements. 
    a | b | a = b             ---------
   ---------------         a |    | XX |
    0 | 0 |   1               ---------
    0 | 1 |   0              | XX |    |
    1 | 0 |   0               ---------
    1 | 1 |   1                     b
Thus it is seen that fuzzy equality corresponds with the following non-trivial arithmetical expression: $$ (a \cap b) \cup (\overline{a} \cap \overline{b}) = (a.b) \cup (1-a)(1-b) = $$ $$ a.b + (1-a)(1-b) - a.b(1-a)(1-b) = a.b + (1-a)(1-b)(1-a.b) = $$ $$ 1 - a - b + a.b + a^2.b + a.b^2 - a^2.b^2 $$ In classical logic the intersection between $(a \cap b)$ and $(\overline{a} \cap \overline{b})$ is zero: the sets $(a \cap b)$ and $(\overline{a} \cap \overline{b})$ are disjoint. Thus $a.b.(1-a)(1-b) = 0$. This means that a suitable fuzzyfication could also be given by: $$ (a \cap b) \cup (\overline{a} \cap \overline{b}) = a.b + (1-a)(1-b) $$ That is: a bilinear interpolation between
$\;\left[\; (0,0) , (1,1) \; \mbox{with equal} = 1 \;\right]\;$ and $\;\left[\; (1,0) , (0,1) \; \mbox{with not equal} = 0 \;\right]\;$ .
There does also exist a 'standard' version of Fuzzy Logic, as can be found at: Union, intersection and complement are defined in this 'standard' version as: $$ \begin{array}{lllll} a \cap b := \min(a,b) & ; & a \cup b := \max(a,b) & ; & \overline{a} := 1 - a \end{array} $$ The Fuzzy Equality is then given by $\;\max(\min(a,b),\min(1-a,1-b))$ .

Find the Differences

An application of Fuzzy Equality as a part of Fuzzy Logic is the detection of differences between almost equal pictures:

Programming notes. After loading the two pictures, it must be found out what pixels share the same position (approximately). This is an art in itself which shall not be described here. Having done that, all (grey-valued) pixel colors are converted to equivalent number values in the range $\,\left[0,1\right]$ , giving numbers $\,a\,$ for picture $(1)$ and numbers $\,b\,$ for picture $(2)$. These are fed into the Fuzzy Equality routine, with numbers in the same $\,\left[0,1\right]\,$ range as the output: 

function Fuzzy_Equality(method : integer; a,b : double) : double;
{
  Fuzzy Equality
}
var
  v : double;

function max(x,y : double) : double;
var
  m : double;
begin
  m := x; if m < y then m := y;
  max := m;
end;

function min(x,y : double) : double;
var
  m : double;
begin
  m := x; if m > y then m := y;
  min := m;
end;

begin
  v := 0;
  case method of
{ Probablistic }
  0 : v := a\*b + (1-a)\*(1-b)\*(1-a\*b);
{ Bilinear }
  1 : v := a\*b + (1-a)\*(1-b);
{ Standard }
  2 : v := max(min(a,b),min(1-a,1-b));
  end;
  Fuzzy_Equality := v;
end;
The outputs are converted to equivalent $\color{red}{\mbox{reddish}}$ colors: the more unequal the pixel greys, the more reddish. In this way, the pixel positions with most different grey values are emphasized as the most reddish spots in the leftmost picture:

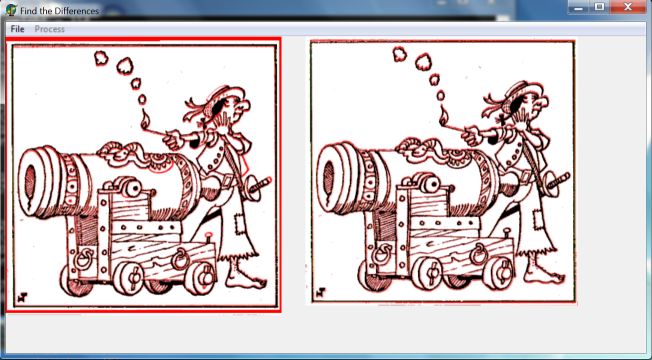
It can be shown experimentally that any version of the above Fuzzy Equalities seems to work equally well. So the fuzzyfication of boolean logic is not quite unambiguous. This is a common feature with "going back to reality", as is exemplified numerous times with e.g. Numerical Analysis: there exist many numerical approximations for the same differential equation.

Update. Maybe the picture example as stated is not (yet) the logic as expected by the OP.
How then about the following logic (yes?) question: How much equal are the two pictures?
An answer is produced by the program if we add all fuzzy equality numbers together and divide by the number of pixels. Resulting in: 

 8.23370043338440E-0001 : Fuzzy Logic method 0
 8.28104562088338E-0001 : Fuzzy Logic method 1
 8.31005249431013E-0001 : Fuzzy Logic method 2
The outcomes are not much different from each other, as expected. So the two pictures are $\,82.3\%$ , $82.8\%$ , $83.1\%$ equal, dependent on the fuzzy equality method chosen.