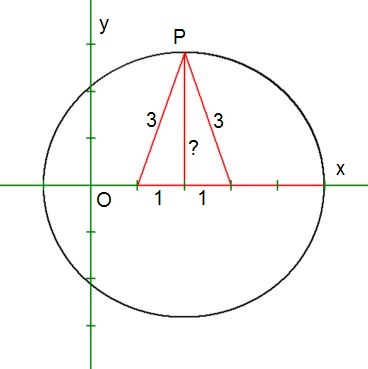
Determining conic section equation given foci and sum of distance to each point
It's not extremely difficult, just take care not to have a square root everywhere:
$$
\sqrt{(x-1)^2+y^2}+\sqrt{(x-3)^2+y^2}=6 \\
\sqrt{(x-1)^2+y^2} = 6 - \sqrt{(x-3)^2+y^2} \\
(x-1)^2+y^2 = 36 + (x-3)^2+y^2 - 12\sqrt{(x-3)^2+y^2} \\
x^2-2x+1+y^2-36-(x^2-6x+9)-y^2 = -12\sqrt{(x-3)^2+y^2} \\
-12\sqrt{(x-3)^2+y^2} = 4x-44 \\
9\left[x^2-6x+9+y^2\right] = (x-11)^2 \\
8x^2-32x+9y^2=40 \\
8(x-2)^2+9y^2=72 \\
(x-2)^2/9+y^2/8=1 \\
\left(\frac{x-2}{3}\right)^2+\left(\frac{y}{2\sqrt{2}}\right)^2 = 1
$$
An ellipse with midpoint $(2,0)$ and axes $(3,2\sqrt{2})$ :