Finding value of 1 variable in a 3-variable $2^{nd}$ degree equation

Disclaimer. Sure I understand what the true question is about, but I thought this would help. And it has helped because the OP changed integers into "positive integers". In order to prevent a bounty from being assigned automatically: don't upvote too much :-(

The equation can be rewritten as: $$ F(a,b) = a^2+b^2 - q(ab-1) = 0 $$ If we now interpret $\,(a,b)\,$ as real valued coordinates, then pictures can be made for the curve $\,F(a,b) = 0$ . Where $\color{green}{green}$ means $\,F(a,b)<0\,$ and $\color{red}{red}$ means $\,F(a,b)>0\,$ . Two cases are distinguished: $\,q > 0\,$ and $\,q < 0$ ; nowhere it has been said that the integers are positive.

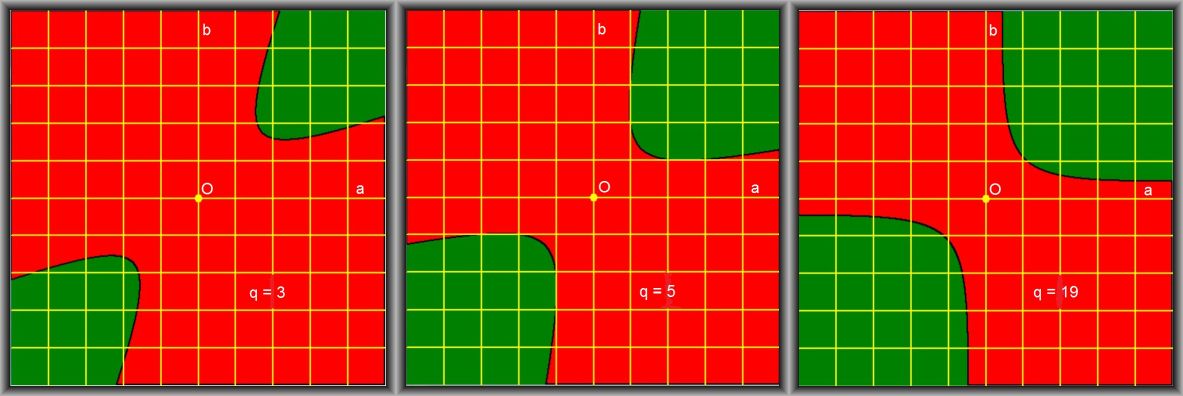
Pictures of $\,F(a,b)=0\,$ for the case $\,q > 0$ , to be precise $\,q=3$ , $q=5$ , $q=19$ :

The case $\,q=0\,$ is trivial: it follows that $\,x=y=0$ .
The case $\,q=1\,$ implies that there is no curve $\,F(a,b)=0$ : $\,a^2+b^2-ab+1=(a-b)^2/2+(a^2+b^2)/2+1 > 0\,$ .
The case $\,q=2\,$ implies that there is no curve $\,F(a,b)=0$ : $\,a^2+b^2-2ab+2=(a-b)^2+2 > 0\,$ .
The case $\,q=3\,$ is the first interesting case for $\,q > 0$ .
All curves for $\,q \ge 3\,$ are hyperbolas, because they have the form of a conic section equation and the discriminant - similar to the one in $\,Ax^2+Bxy+Cy^2+Dx+Ey+F=0\,$ is : $\,B^2-4AC = q^2-4 > 0$ .

Pictures of $\,F(a,b)=0\,$ for the case $\,q < 0$ , to be precise $\,q=-1$ , $q=-2$ , $q=-10$ :

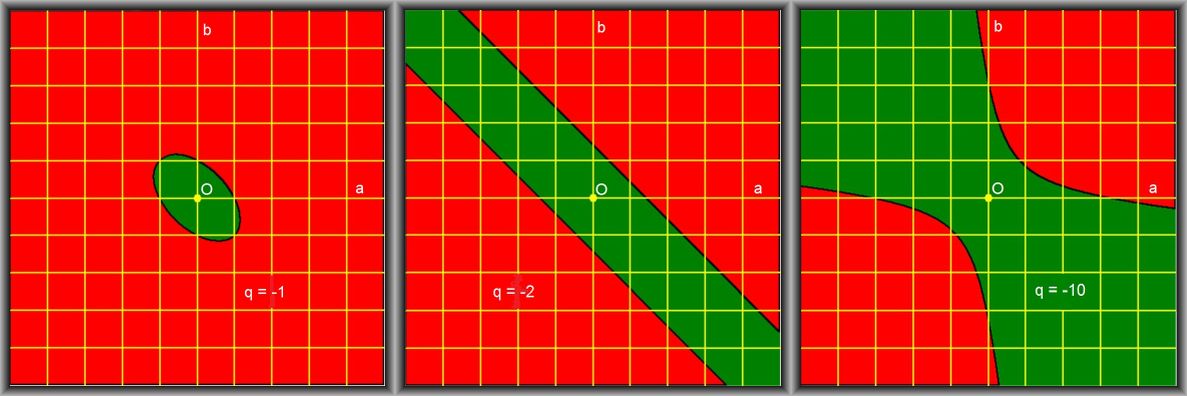
The case $\,q=-1\,$ implies that the curve $\,F(a,b)=0\,$ is an ellipse : $\,a^2+b^2+ab-1=0\,$ , namely a conic section with discriminant $= -3$ .
The case $\,q=-2\,$ implies that $\,F(a,b)=0\,$ is a degenenerate conic section: $\,a^2+b^2+2ab-2=0$ $\Longrightarrow\;$ $a+b = \pm\sqrt{2}$ , i.e. two parallel straight lines.
The hyperbolas are back in town with $\,q < -2$ .

About the integer solutions. Educated guess from the pictures:
$q=5 \;\Longrightarrow \;(a,b) = (2,1) \vee (1,2) \vee (-2,-1) \vee (-1,-2)$ .
$q=5 \;\Longrightarrow \;(a,b) = (3,1) \vee (1,3) \vee (-3,-1) \vee (-1,-3)$ .
$q=-1 \; \Longrightarrow \; (a,b) = (0,1) \vee (1,0) \vee (-1,0) \vee (0,-1)$ .

Update. The following Pascal program snippet indeed shows that there are at least many solutions $\,(a,b)\,$ for $\,q=5$ : 

program infinity;

Uses SysUtils;

function g(a,b : integer) : integer;
const
  q : integer = 5;
begin
  g := sqr(a)+sqr(b)-q*(a*b-1);
end;

function stop(x,y : integer) : boolean;
begin
  stop := (Length(IntToStr(x)) > 9)
       or (Length(IntToStr(y)) > 9);
end;

procedure crawler;
var
  x,y,f : integer;
begin
  x := 1; y := 1;
  while true do
  begin
    y := y + 1;
    f := g(x,y);
    if f = 0 then Writeln(x,' ',y);
    while f > 0 do
    begin
      x := x + 1;
      f := g(x,y);
      if f = 0 then Writeln(x,' ',y);
    end;
    if (f = 0) and stop(x,y) then Break;
  end;
end;

begin
  crawler;
end.
Output $\,a\;b$ , apart from the last (= overflow) record: 
1 2
1 3
2 9
3 14
9 43
14 67
43 206
67 321
206 987
321 1538
987 4729
1538 7369
4729 22658
7369 35307
22658 108561
35307 169166
108561 520147
169166 810523
520147 2492174
810523 3883449
2492174 11940723
3883449 18606722
11940723 57211441
18606722 89150161
57211441 274116482
89150161 427144083
There is a lucid structure observed in the above sequence.
If the subsequent values of $\,a\,$ are numbered as $\,a_1,a_2,a_3,\cdots\,$ and if the subsequent values of $\,b\,$ are numbered as $\,b_1,b_2,b_3,\cdots\,$ , then it seems that we have: $\,\forall n : a_{n+2} = b_n$ .
Let's solve some equations, to see where this may come from: $$ a^2+b^2-5(ab-1) = 0 \quad \Longrightarrow \quad b = \frac{5a}{2} \pm \frac{\sqrt{21a^2-20}}{2} $$ Now start with $\,a_1=a_2=1$ : $$ b_1 = \frac{5}{2} - \frac{\sqrt{21-20}}{2} = 2 \\ b_2 = \frac{5}{2} + \frac{\sqrt{21-20}}{2} = 3 $$ Giving the first two records in the output. However, the equation $\,a^2+b^2-5(ab-1) = 0\,$ is symmetric in $\,(a,b)\,$ , so the values of $\,b\,$ are at the same time new values of $\,a\,$ . Thus we can proceed with $\,a_3=2\,$ and $\,a_4=3\,$ : $$ \frac{5\cdot 2}{2} - \frac{\sqrt{21\cdot2^2-20}}{2} = 1 = a_1 \quad ; \quad \frac{5\cdot 2}{2} + \frac{\sqrt{21\cdot2^2-20}}{2} = 9 = b_3\\ \frac{5\cdot 3}{2} - \frac{\sqrt{21\cdot3^2-20}}{2} = 1 = a_2 \quad ; \quad \frac{5\cdot 3}{2} + \frac{\sqrt{21\cdot3^2-20}}{2} = 14 = b_4 $$ It becomes clear that the minus signs will reproduce old results. Hence, recursively, starting with $\,(a_1,b_1),(a_2,b_2)$ and $q=5$ : $$ a_{n} = b_{n-2} \quad ; \quad b_{n} = \frac{5 a_n}{2} + \frac{\sqrt{21 a_n^2 - 20}}{2} = q\,a_n-a_{n-2} = \frac{a_n^2+q}{a_{n-2}} $$ That is for $\;\forall n \in \mathbb{N}\,$ with $\,n > 2$ .