How prove this diophantine equation have only three integer solution?

How prove this diophantine equation $(x^2-y)(y^2-x)=(x+y)^2$ have only three integer solution?

Please don't vote. Just a pictural comment to show what the curve $(x^2-y)(y^2-x)-(x+y)^2=0$ does look like ( : it's an "elbow" ) .

![enter image description here][2]

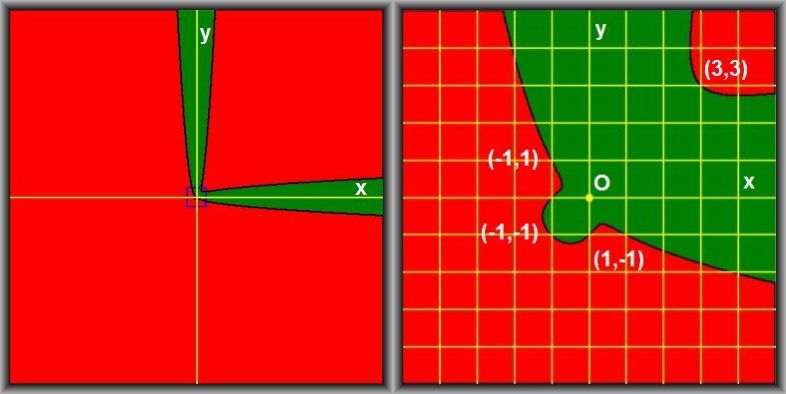
$\color{red}{Red}$ is positive, $\color{green}{green}$ is negative. The integer coordinates are yellow lines.
Picture on the right is $\color{blue}{blue}$ rectangle in picture on the left zoomed in $20 \times$ .