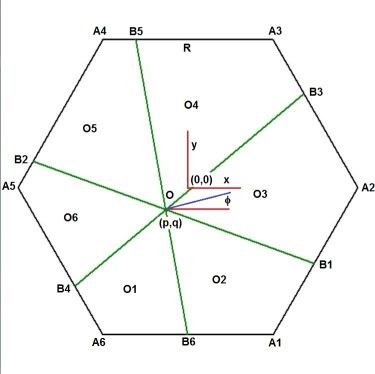
Definitions.
Origin in the middle of the hexagon, $O = (p,q)$ ,
angle of normal $\overline{B_5 B_6}$ with x-axis $= \phi$ .
Equations.
$$
\begin{array}{l}
\overline{B_5 B_6} \quad : \quad \cos(\phi)(x-p)+\sin(\phi)(y-q) = 0 \\
\overline{B_1 B_2} \quad : \quad \cos(\phi+\pi/3)(x-p)+\sin(\phi+\pi/3)(y-q) = 0 \\
\overline{B_3 B_4} \quad : \quad \cos(\phi-\pi/3)(x-p)+\sin(\phi-\pi/3)(y-q) = 0
\end{array}
$$
Edges of the hexagon, assuming that the length of an edge $= R\,$ and $\;0 \le \lambda \le 1$ :
$$
\begin{array}{l}
\overline{A_6 A_1} \quad : \quad (x,y) = (A_6^x,A_6^y) + \lambda (\vec{A_1}-\vec{A_6}) = (-R/2,-R\sqrt{3}/2) + \lambda (R,0) \\
\overline{A_1 A_2} \quad : \quad (x,y) = (A_1^x,A_1^y) + \lambda (\vec{A_2}-\vec{A_1}) =(R/2,-R\sqrt{3}/2) + \lambda (R/2,R\sqrt{3}/2) \\
\overline{A_2 A_3} \quad : \quad (x,y) = (A_2^x,A_2^y) + \lambda (\vec{A_3}-\vec{A_2}) =(R,0) + \lambda (-R/2,R\sqrt{3}/2) \\
\overline{A_3 A_4} \quad : \quad (x,y) = (A_3^x,A_3^y) + \lambda (\vec{A_4}-\vec{A_3}) =(R/2,R\sqrt{3}/2) + \lambda (-R,0) \\
\overline{A_4 A_5} \quad : \quad (x,y) = (A_4^x,A_4^y) + \lambda (\vec{A_5}-\vec{A_4}) =(-R/2,R\sqrt{3}/2) + \lambda (-R/2,-R\sqrt{3}/2) \\
\overline{A_5 A_6} \quad : \quad (x,y) = (A_5^x,A_5^y) + \lambda (\vec{A_6}-\vec{A_5}) =(-R,0) + \lambda (R/2,-R\sqrt{3}/2)
\end{array}
$$
Determine intersection points of lines $\overline{B_i B_j}$ with hexagon
edges $\overline{A_i A_j}$ as appropriate. Introduce $\tan(\phi)$ instead
of $\cos(\phi)$ and $\sin(\phi)$ , and put $\;\tan(\phi) = t$ .
For example $\overline{B_1B_2}$ with $\overline{A_1A_2}$ :
$$
\cos(\phi+\pi/3)(\left[R/2 +\lambda R/2\right]-p)
+\sin(\phi+\pi/3)(\left[-R\sqrt{3}/2 +\lambda R\sqrt{3}/2\right]-q) = 0
\quad \Longrightarrow \\
\lambda = \frac{\cos(\phi+\pi/3)(-R/2+p)
+\sin(\phi+\pi/3)(R\sqrt{3}/2+q)}
{\cos(\phi+\pi/3)R/2+\sin(\phi+\pi/3)R\sqrt{3}/2} =\\
1/2+1/2\,{\frac {p}{R}}+1/2\,{\frac {\sin \left( \phi \right) \sqrt {3
}}{\cos \left( \phi \right) }}-1/2\,{\frac {\sin \left( \phi \right)
\sqrt {3}p}{R\cos \left( \phi \right) }}+1/2\,{\frac {\sin \left( \phi
\right) q}{R\cos \left( \phi \right) }}+1/2\,{\frac {\sqrt {3}q}{R}} \quad
\Longrightarrow \\ \lambda =
1/2+1/2\,{\frac {p}{R}}+1/2\,t\sqrt {3}-1/2\,{\frac {\sqrt {3}pt}{R}}+
1/2\,{\frac {qt}{R}}+1/2\,{\frac {\sqrt {3}q}{R}}
$$
Substitute $\,\lambda\,$ into $\;(x,y)=(R/2,-R\sqrt{3}/2)+\lambda(R/2,R\sqrt{3}/2)\;$
to find $\,(B_1^x,B_1^y)$ . Likewise all the other coordinates:
$$
\begin{array}{l}
B_6^x = -1/2\,R+ \left( 1/2+{\frac {p}{R}}+1/2\,t\sqrt {3}+{\frac {qt}{R}}
\right) R \quad ; \quad B_6^y = -1/2\,R\sqrt {3} \\
B_5^x = -1/2\,R+ \left( 1/2+{\frac {p}{R}}-1/2\,t\sqrt {3}+{\frac {qt}{R}}
\right) R \quad ; \quad B_5^y = 1/2\,R\sqrt {3} \\
B_1^x = 1/2\,R+1/2\, \left( 1/2+1/2\,{\frac {p}{R}}+1/2\,t\sqrt {3}-1/2\,{
\frac {\sqrt {3}pt}{R}}+1/2\,{\frac {qt}{R}}+1/2\,{\frac {\sqrt {3}q}{
R}} \right) R \\
B_1^y = -1/2\,R\sqrt {3} \left( 1/2-1/2\,{\frac {p}{R}}-1/2\,t\sqrt {3}+1/2\,{
\frac {\sqrt {3}pt}{R}}-1/2\,{\frac {qt}{R}}-1/2\,{\frac {\sqrt {3}q}{
R}} \right) \\
B_2^x = -1/2\,R-1/2\, \left( 1/2-1/2\,{\frac {p}{R}}+1/2\,t\sqrt {3}+1/2\,{
\frac {\sqrt {3}pt}{R}}-1/2\,{\frac {qt}{R}}-1/2\,{\frac {\sqrt {3}q}{
R}} \right) R \\
B_2^y = 1/2\,R\sqrt {3} \left( 1/2+1/2\,{\frac {p}{R}}-1/2\,t\sqrt {3}-1/2\,{
\frac {\sqrt {3}pt}{R}}+1/2\,{\frac {qt}{R}}+1/2\,{\frac {\sqrt {3}q}{
R}} \right) \\
B_3^x = 1/2\,R+1/2\, \left( -1/2\,t\sqrt {3}+1/2\,{\frac {\sqrt {3}pt}{R}}+1/2
+1/2\,{\frac {p}{R}}-1/2\,{\frac {\sqrt {3}q}{R}}+1/2\,{\frac {qt}{R}}
\right) R \\
B_3^y = 1/2\,R\sqrt {3} \left( 1/2+1/2\,t\sqrt {3}-1/2\,{\frac {\sqrt {3}pt}{R
}}-1/2\,{\frac {p}{R}}+1/2\,{\frac {\sqrt {3}q}{R}}-1/2\,{\frac {qt}{R
}} \right) \\
B_4^x = -R+1/2\, \left( 1/2\,t\sqrt {3}+1/2\,{\frac {\sqrt {3}pt}{R}}+1/2+1/2
\,{\frac {p}{R}}-1/2\,{\frac {\sqrt {3}q}{R}}+1/2\,{\frac {qt}{R}}
\right) R \\
B_4^y = -1/2\,R\sqrt {3} \left( 1/2\,t\sqrt {3}+1/2\,{\frac {\sqrt {3}pt}{R}}+
1/2+1/2\,{\frac {p}{R}}-1/2\,{\frac {\sqrt {3}q}{R}}+1/2\,{\frac {qt}{
R}} \right)
\end{array}
$$
The areas are calculated with determinants; $O_1$ as an example:
$$
2\,O_1 = -(B_4^x-A_6^x)(B_6^y-A_6^y)+(B_4^y-A_6^y)(B_6^x-A_6^x)
+ (B_4^x-p)(B_6^y-q)-(B_4^y-q)(B_6^x-p)
$$
Giving rise to the following equations:
$$
\begin{array}{l}
O_1 = 1/4\,{R}^{2}\sqrt {3}-3/8\,{p}^{2}t+3/4\,qR+3/4\,pq+1/4\,\sqrt {3}pR-3
/4\,tRp+1/4\,\sqrt {3}Rqt-1/4\,\sqrt {3}pqt-1/8\,\sqrt {3}{p}^{2}+1/8
\,\sqrt {3}{q}^{2}+3/8\,{q}^{2}t = 1363 \\
O_2 = 1/4\,{R}^{2}\sqrt {3}+3/8\,{p}^{2}t+3/4\,qR-3/4\,pq-1/4\,\sqrt {3}pR-3
/4\,tRp-1/4\,\sqrt {3}Rqt-1/4\,\sqrt {3}pqt-1/8\,\sqrt {3}{p}^{2}+1/8
\,\sqrt {3}{q}^{2}-3/8\,{q}^{2}t = 1775 \\
O_3 = 1/4\,\sqrt {3} \left( -2\,pR+{p}^{2}+{R}^{2}-{q}^{2}-2\,Rqt+2\,pqt
\right) = 3115 \\
O_4 = -3/8\,{p}^{2}t-1/4\,\sqrt {3}pR+3/4\,pq-3/4\,qR-1/8\,\sqrt {3}{p}^{2}+
1/4\,{R}^{2}\sqrt {3}+3/8\,{q}^{2}t+1/8\,\sqrt {3}{q}^{2}-1/4\,\sqrt {
3}Rqt-1/4\,\sqrt {3}pqt+3/4\,tRp = 4067 \\
O_5 = 3/8\,{p}^{2}t+1/4\,\sqrt {3}pR-3/4\,pq-3/4\,qR-1/8\,\sqrt {3}{p}^{2}+1
/4\,{R}^{2}\sqrt {3}-3/8\,{q}^{2}t+1/8\,\sqrt {3}{q}^{2}+1/4\,\sqrt {3
}Rqt-1/4\,\sqrt {3}pqt+3/4\,tRp = 3127 \\
O_6 = 1/4\,\sqrt {3} \left( 2\,pR+{p}^{2}+{R}^{2}-{q}^{2}+2\,Rqt+2\,pqt \right) = 1763
\end{array}
$$
These are $6$ equations $\;(O_1,O_2,O_3,O_4,O_5,O_6) = (0,0,0,0,0,0)\;$
with $3$ unknowns $\;(p,q,t)\;$ , typically an over-determined system.
Let's first substitute the real length of the hexagon edges:
$$
R = \sqrt{15210/(3\sqrt{3}/2)}
$$
If we now solve only the first three $\;(O_1,O_2,O_3) = (0,0,0)\;$
then we get two exact solutions with our computer algebra system.
One of these involves a tangent $\,t \approx -1.427142752$ , corresponding
with too large an angle of $\;-55^\circ$ . The other solution must be the
right one:
$$
p = -\frac{42\sqrt{5\sqrt{3}}}{13} \quad ; \quad
q = -\frac{46\sqrt{5\sqrt{3}}\sqrt{3}}{13} \quad ; \quad
t = \frac{\sqrt{3}}{45}
$$
And here come the corresponding areas, exactly as they are in the OP's picture :
O1 = 1363. O2 = 1775. O3 = 3115.
O4 = 4067. O5 = 3127. O6 = 1763.
At last, we calculate the lengths $\,x\,$ of the $\,\overline{B_i B_j}$ .
Indeed they are all the same and they are only dependent upon
the (tangent $\,t\,$ of the) angle $\phi$ :
$$
x = \sqrt{3 R^2 (t^2+1)} \times 15/R = \huge 26.
$$
Where the scaling factor with respect to $\overline{A_1A_2} = 15$
has been taken into account.
