The statement is valid not only for rotations. According to relativity,
there is no preferred frame of reference / coordinate system.
Therefore, in kinematics, all (times and) positions and motions are relative. (Dynamics - with forces - is another matter).
Consider a two-dimensional example, as has been found in a book about
Computer Graphics (to be precise: J.D. Foley, A. van Dam, Fundamentals
of Interactive Computer Graphics, 1982). There are two frames of reference,
one attached to the observer (world), one attached to an object (chair):
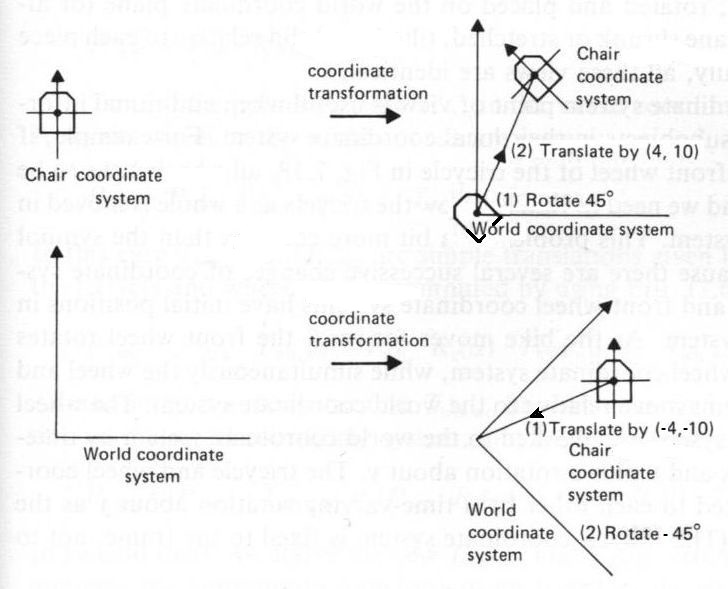
With a transformation of coordinates, the only thing that is important is the
relative position of the object with respect ot the observer. This means that
the end result of a coordinate transformation can be achieved in at least two ways.
As is displayed in the example:
-
Extrinsic.
Rotate $\,R\,$ the chair in the world coordinate system over an angle of $45^o$
and then Translate $\,T\,$ it over a distance $(4,10)$. Thus resulting in a transformation $\,TR$ .
-
Intrinsic.
Translate $\,T^{-1}\,$ the observer in the chair coordinate system over a distance
$(-4,-10)$ and then rotate $\,R^{-1}\,$ the world coordinate system over an angle $-45^o$.
Thus resulting in a transformation $\,R^{-1}T^{-1}$ .
With this simple example, we can see immediately that the transformations
are the inverse of each other: $\,R^{-1}T^{-1}= (TR)^{-1}$ .
Hope you get the idea.
Generalizing this to three dimensions is expected to be a matter of filling in the
(somewhat more involved) technicalities.
Update. Hmm, "not quite a proof". Then perhaps this.
Let the coordinate system of the object be called $O$ and the world coordinate
system be called $W$. Both coordinate systems are coincident in the beginning.
The first step is to apply a transformation $R$ to $O$
(just as in the example, but in general now).
The second step is to make $W$
coincident again with $O$, which is done by applying the same transformation
$R$ to $W$ as has been done in the first step with $O$.
Then effectively nothing
has changed and we have the original configuration again: the product of step (1)
and step (2) is the identity.
It is thus obvious that
the first step could also have been accomplished by applying the inverse $R^{-1}$
transformation to $W$ instead of $O$.
Common
properties of inverse operations like $(AB)^{-1}= B^{-1}A^{-1}$ are assumed throughout to be well known.
This completes the proof.

