Try a convolution with a function of small width and great height
(: Richard P. Feynman in 'Space-Time Approach to Quantum Electrodynamics').
Name this function $\delta(x)$ (not quite by coincidence).
The simplest one is $\,\delta(x) = B(x/\sigma)/\sigma\,$ where $\sigma \rightarrow 0$ and:
$$
B(t) = \left\{ \begin{array}{lll}
0 & \mbox{for} & t \le -1/2 \\
1 & \mbox{for} & -1/2 \le t \le +1/2 \\
0 & \mbox{for} & +1/2 \le t
\end{array} \right.
$$
The geometry of $\,\delta(x)\,$ is a rectangle with height $1/\sigma$ and width $\sigma$ ,
resulting in an area $1$, thus establishing that the function $\,\delta(x)\,$ is normed.
Now define:
$$ \overline{f}(x) =
\int_{-\infty}^{+\infty} \delta(x-t)\,f(t)\,dt
= \frac{1}{\sigma} \int_{x-\sigma/2}^{x+\sigma/2} f(t)\,dt
$$
This is what we find:
$$
\overline{f}(x) = \left\{ \begin{array}{lll}
x/x_s & \mbox{for} & x \le x_s-\sigma/2 \\
P(x) & \mbox{for} & x_s-\sigma/2 \le x \le x_s+\sigma/2 \\
(1-x)/(1-x_s) & \mbox{for} & x_s+\sigma/2 < x
\end{array} \right.
$$
Where the (piece of a) parabola $\,P(x)\,$ is defined as:
$$ P(x) =
\frac{1}{\sigma}\int_{x-\sigma/2}^{x_s} \frac{t}{x_s}\,dt +
\frac{1}{\sigma}\int_{x_s}^{x+\sigma/2} \frac{1-t}{1-x_s}\,dt = \\
\frac {4\,{{\it x_s}}^{2}+4\,{x}^{2}-4\,x\sigma+8\,x\sigma\,{
\it x_s}+{\sigma}^{2}-8\,{\it x_s}\,x-4\,\sigma\,{\it x_s}}{8\sigma
\,{\it x_s}\, \left( -1+{\it x_s} \right) }
$$
Thus, with the simplest convolution kernel, the result is a piecewise analytic
function. The original $\,f(x)\,$ is in black, the convoluted one
$\,\overline{f}(x)\,$ is in $\color{red}{\mbox{red}}$, $\,x_s\,$ is chosen at random and $\,\sigma = 1/10\,$ in the renditions depicted here:
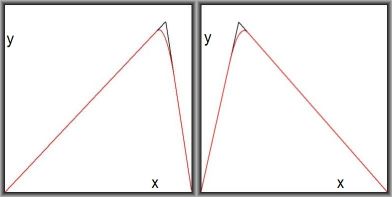
A nice property of the convolution is that $\overline{f}(x)$ inherits the smoothness
of the kernel. One might alternatively define that kernel as a Gauss function. Thus:
$$ \overline{f}(x) =
\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^{+\infty}
e^{-\frac{1}{2}(x-t)^2/\sigma^2} f(t)\,dt
$$
This results in a not so simple expression, but the advantage is that
$\overline{f}(x)$ is truly analytic. I leave this as an exercise to the reader.
Visualization does not differ much from the ones given.

