How to prove this inequality $\sum\limits_{cyc}\frac{x+y}{\sqrt{x^2+xy+y^2+yz}}\ge 2+\sqrt{\frac{xy+yz+xz}{x^2+y^2+z^2}}$

This is a question of the symmetric type, such as listed in: With a constraint $\;x+y+z=1\;$ and $\;x,y,z > 0$ . Sort of a general method to transform such a constraint into the inside of a triangle in 2-D has been explained at length in:

Our function $f$ in this case is: $$ f(x,y,z) = \dfrac{x+y}{\sqrt{x^2+xy+y^2+yz}}+\dfrac{y+z}{\sqrt{y^2+yz+z^2+zx}}+\dfrac{z+x}{\sqrt{z^2+zx+x^2+xy}} - \left[2+\sqrt{\dfrac{xy+yz+xz}{x^2+y^2+z^2}}\right] $$

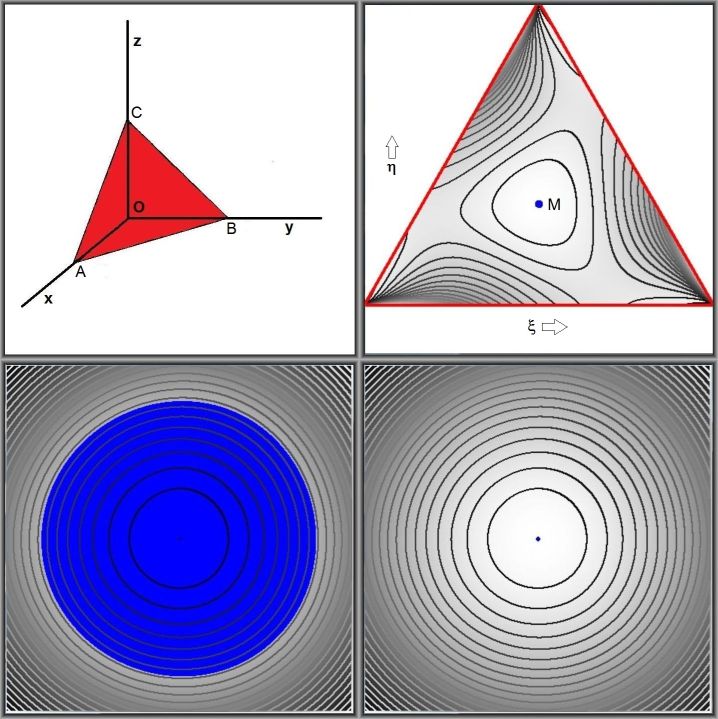
Places where $\;|f(x,y,z)|\;$ is less than, say, $\;\epsilon\;$ ("eps", see below), are colored $\color{blue}{blue}$. The blue spots in the pictures are a proof without words that the only minimum is indeed close to zero and near the midpoint $M$ of the equilateral triangle: $(x_M,y_M,z_M) = (1/3,1/3,1/3)$ .

A few further details: 
A = (1,0,0); O = (0,0,0);                        eps := 0.0003;
B = (0,1,0); M = (1/3,1/3,1/3);                  xmin := -0.7; xmax := 0.7;
C = (0,0,1);                                     ymin := -0.6; ymax := 0.8;

xmin := -0.02; xmax := 0.02;                     eps := eps/4096;
ymin := -0.02; ymax := 0.02;
Two or three iterations result in pictures that, quite remarkably, can hardly be distinguished from the two pictures at the bottom: 
xmin := xmin/64; xmax := xmax/64;                eps := eps/4096;
ymin := ymin/64; ymax := ymax/64;
With calculations ending in a "range check error" because $\epsilon$ ( = eps) has become zero (too) quickly. Which - alright? - is a proof of the statement up to no less than machine precision.

A local and planar orthogonal coordinate system for the equilateral triangle can be obtained as: $$ \vec{e}_\xi = \vec{OB}-\vec{OA} = \left[ \begin{array}{c} -1 \\ +1 \\ 0 \end{array} \right] / \sqrt{2}\\ \vec{e}_\eta = \vec{OC}-\left(\vec{OA}+\vec{OB}\right)/2 = \left[ \begin{array}{c} -1/2 \\ -1/2 \\ +1 \end{array} \right] / \sqrt{3/2} $$ Giving for the relationship between global coordinates $(x,y,z)$ and local triangle coordinates $(\xi,\eta)$: $$ x = -\frac{1}{\sqrt{2}} \xi -\frac{1}{\sqrt{6}} \eta + \frac{1}{3}\\ y = +\frac{1}{\sqrt{2}} \xi -\frac{1}{\sqrt{6}} \eta + \frac{1}{3}\\ z = \sqrt{\frac{2}{3}} \eta + \frac{1}{3} $$ It's easily verified that $x+y+z=1$ ; the origin of the local coordinate system is at $(\xi,\eta) = (0,0)$ . In this way, the function can be expressed in local triangle coordinates, but (at least for me) that didn't simplify the puzzle much.

A common method to study the function $f(x,y,z)$ in the neighborhood of $M$ is to take derivatives at that point (without a computer algebra system it's a tedious job). To begin with, the zero'th order derivative is zero: $$ f(M) = 0 $$ The first order derivatives are zero as well, meaning that there is an extremum to be expected there: $$ \left[ \begin{array}{c} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \\ \frac{\partial f}{\partial z} \end{array} \right] (M) = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right] $$ The second order derivatives are summarized as a Hessian matrix: $$ \left[ \begin{array}{ccc} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^ f}{\partial x \partial y} & \frac{\partial^2 f}{\partial x \partial z} \\ \frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^ f}{\partial y^2} & \frac{\partial^2 f}{\partial y \partial z} \\ \frac{\partial^2 f}{\partial z \partial x} & \frac{\partial^ f}{\partial z \partial y} & \frac{\partial^2 f}{\partial z^2} \end{array} \right] (M) = \frac{51}{64} \left[ \begin{array}{ccc} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{array} \right] $$ Therefore $f(x,y,z)(M)$ can be approximated by the following Taylor series expansion: $$ f(x,y,z)(M) \approx \frac{51}{32} \left( x^2 + y^2 + z^2 - x y - x z - y z \right) $$ To investigate the nature of this expression, eigenvalues and eigenvectors of the Hessian matrix are determined: $$ \left| \begin{array}{ccc} 2-\lambda & -1 & -1 \\ -1 & 2-\lambda & -1 \\ -1 & -1 & 2-\lambda \end{array} \right| = -\lambda^3 + 6 \lambda^2 - 9\lambda = 0 \qquad \Longrightarrow \qquad \lambda \in \left\{ 0,3 \right\} $$ The normed eigenvector corresponding with $\;\lambda=0\;$ is $\;(1,1,1)/\sqrt{3}\;$ and the normed eigenvectors corresponding with $\;\lambda=3\;$ is anything in the plane $\;x+y+z=0\;$ , which is parallel to the plane of our equilateral triangle. So we can choose the local triangle coordinate system for the latter: $$ \vec{e}_\xi = \left[ \begin{array}{c} -1 \\ +1 \\ 0 \end{array} \right] / \sqrt{2} \qquad \vec{e}_\eta = \left[ \begin{array}{c} -1/2 \\ -1/2 \\ +1 \end{array} \right] / \sqrt{3/2} \qquad \vec{e}_\zeta = \left[ \begin{array}{c} +1 \\ +1 \\ +1 \end{array} \right] / \sqrt{3} $$ If we express the "conic section" into those local coordinates, then what we get is the following: $$ x^2 + y^2 + z^2 - x y - x z - y z = 3 \xi^2 + 3 \eta^2 = \frac{\xi^2}{1/3} + \frac{\eta^2}{1/3} + \frac{\zeta^2}{\infty} $$ The iso-surfaces are a circular cylinder with axis in the direction of $\;\vec{OM} = (1,1,1)/3 $ . Thus, as a first approximation, the isolines in the neighborhood of $M$ must be circles, which is exactly what's observed in the above pictures: $$ f(x,y,z)(M) \approx \frac{153}{32} \left( \xi^2 + \eta^2 \right) \qquad \mbox{for} \qquad x+y+z=1 $$ Behaviour of the abovementioned iterations is explained quite well with this theory. It is also trivial that the only minimum found with this approximation is $\,0\,$ at the midpoint $M$ with $(\xi,\eta) = (0,0)$ .
Guess something more is needed, though, to convert the last argument into a die hard proof.