This is actually the
duplicate of an answer to the following question:
Proving that for each two parabolas, there exists a transformation taking one to the other .
According to the theory presented there, it is advantageous to write the OP's equation as follows:
$$
2(x-y) = \frac{1}{2} (x+2y)^2 \qquad \mbox{or} \qquad \eta = \frac{1}{2} \xi^2
$$
Where it is noted that $\;\xi\;$ physically corresponds with "time" . Anyway, it follows that:
$$
\left\{ \begin{array}{l} \xi = x+2y \\ \eta = 2(x-y) \end{array}\right.
\qquad \Longleftrightarrow \qquad
\left\{ \begin{array}{l}
x = \frac{1}{3}\xi + \frac{1}{3}\eta \\
y = \frac{1}{3}\xi - \frac{1}{6}\eta
\end{array}\right.
$$
Giving the "velocities", "accelerations" and "origin" in the parameter equations of the parabola.
$$
v_x = v_y = \frac{1}{3} \quad ; \quad
a_x = \frac{1}{3} \quad ; \quad
a_y = - \frac{1}{6} \quad ; \quad
s_x = s_y = 0
$$
In matrix form:
$$
\left[ \begin{array}{c} x \\ y \end{array} \right] =
\left[ \begin{array}{cc} v_x & a_x \\ v_y & a_y \end{array} \right]
\left[ \begin{array}{c} \xi \\ \xi^2/2 \end{array} \right] =
\left[ \begin{array}{cc} +\frac{1}{3} & +\frac{1}{3} \\ +\frac{1}{3} & -\frac{1}{6} \end{array} \right]
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right]
$$
If you believe that a linear mapping transforms a parabola into a parabola then we are done.Otherwise.
An orthogonal coordinate transformation, still according to
the same theory, is obtained by a parameter shift $\;\tau$ :
$$
\tau = \frac{v_x a_x + v_y a_y}{a^2_x + a^2_y} = \frac{1/3 \cdot 1/3 - 1/3 \cdot 1/6}{1/9 + 1/36} = \frac{2}{5}
$$
Resulting in:
$$
x = (v_x-a_x\tau)\xi + a_x\eta + (\frac{1}{2}a_x\tau^2-v_x\tau+s_x)
= \frac{1}{5}\xi + \frac{1}{3}\eta - \frac{8}{75} \\
y = (v_y-a_y\tau)\xi + a_y\eta + (\frac{1}{2}a_y\tau^2-v_y\tau+s_y)
= \frac{2}{5}\xi - \frac{1}{6}\eta - \frac{11}{75}
$$
In matrix form:
$$
\left[ \begin{array}{c} x \\ y \end{array} \right] =
\left[ \begin{array}{cc} +\frac{1}{5} & +\frac{1}{3} \\
+\frac{2}{5} & - \frac{1}{6} \end{array} \right]
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right] -
\left[ \begin{array}{c} \frac{8}{75} \\ \frac{11}{75} \end{array} \right] =
\left[ \begin{array}{cc} \frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \end{array} \right]
\left[ \begin{array}{c} \frac{1}{\sqrt{5}}\xi \\ -\frac{\sqrt{5}}{6}\eta \end{array} \right] -
\left[ \begin{array}{c} \frac{8}{75} \\ \frac{11}{75} \end{array} \right]
$$
The meaning of this is transforming $\;\eta = \xi^2/2\;$ into the original
$\;(x+2y)^2=4(x-y)\;$ by scaling the $\xi$ coordinate with a factor $1/\sqrt{5}$ ,
scaling the $\eta$ coordinate with a factor $-\sqrt{5}/6$ (i.e. scaling and mirroring),
followed by a rotation over an angle $\;\arctan(2)\;$ and a translation over $\;-(8,11)/75$ .
Nobody will deny that $\;\eta = \xi^2/2\;$ represents a "standard" parabola and these transformations don't change that fact.
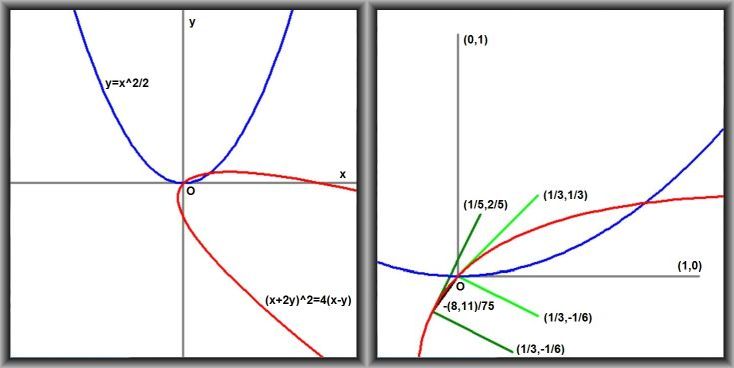
Viewports:
xmin := -5; xmax := 5; xmin := -1/3; xmax := 1.1;
ymin := -5; ymax := 5; ymin := -1/3; ymax := 1.1;
Colors:
- Blue: standard parabola $y = x^2/2$
- Red: original parabola $(x+2y)^2=4(x-y)$
- Grey: global Cartesian coordinate system / unit vectors of standard parabola.
- Lime: non-orthogonal coordinate system / unit vectors if "we are done".
- Green: orthogonal coordinate system if "Otherwise". Note that the system is left handed and that the axis corresponding with "acceleration" does not change / is parallel to the Lime one.
- Black: translation vector $(s_x,s_y)$ corresponding with "time" $\tau$
needed to travel along the (red) parabola from the origin to that position.
A. Einstein: Things should be made as simple as possible. But not simpler.

