The parent question that maybe still remains to be answered at this moment is:
Solve the Diophantine equation $a^2(2^a-a^3)+1=7^b$ .
As far as the parent question is concerned, when generalizing to integer values $\;-\infty < x < +\infty$ ,
it is found that $(0,0)$ and indeed $(10,4)$ are integer solutions
( i.e. the only ones that I have been able to find, with some simple numerical means ).
If we solve $b$ from this equation, rename $b$ to $y$ and $a$ to $x$ , then the following real-valued function results:
$$
y = \ln\left[x^2\left(2^x-x^3\right)+1\right]/\ln(7)
$$
Graphs of the function are depicted below. Red dots indicate integer values $(x,y)$ . The argument of the logarithm is colored "silver".
There are two large red dots $(M,S)$ at the known integer solutions $(0,0)$ and $(10,4)$ of the Diophantine equation.
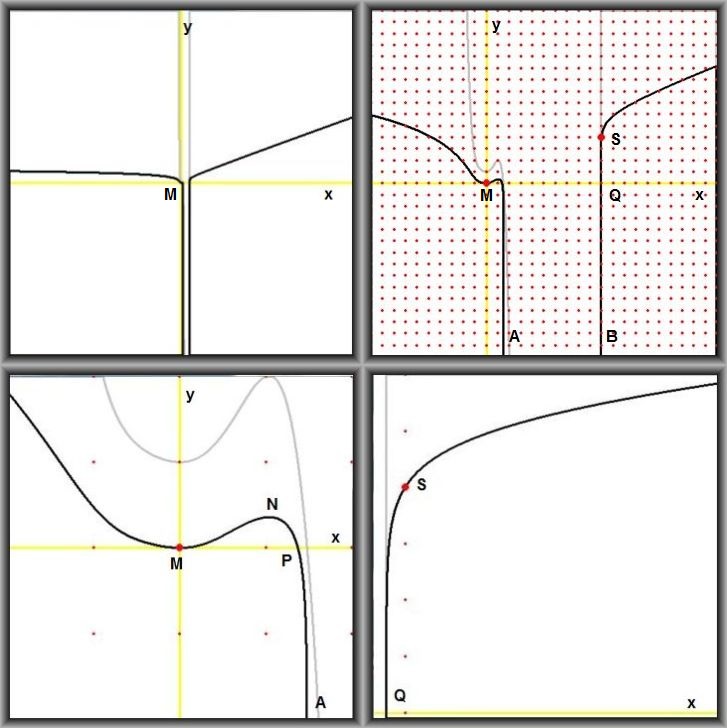
Viewport sizes from left to right / top to bottom:
xmin := -200; xmax := 200;
ymin := -200; ymax := 200;
xmin := -10; xmax := 20;
ymin := -15; ymax := 15;
xmin := -2; xmax := 2;
ymin := -2; ymax := 2;
xmin := 9.90; xmax := 11;
ymin := -0.1; ymax := 6;
Questions:
- There are three zeroes $(M,P,Q)$ ; $M = (0,0)$ is easy. But were are $P$ and $Q$ ?
- There are two extreme values $(M,N)$ ; $M = (0,0)$ is easy. But what is $N=(x_N,y_N)$ ?
- There are two vertical asymptotes $(A,B)$. Between $A$ and $B$ the function is undefined.
Where are $x_A$ and $x_B$ ?
- The steep slope on the right changes into a moderate one. A straight line it seems.
Is that right? If so, what then is the slope of that straight line?
Partial answers, i.e. all values approximately / numerically (with help of MAPLE) :
- Zeroes $P$ and $Q$ of the function are at the solutions of $\;2^x-x^3 = 0$ .
We find: $x_P=1.373467120\;$ for $\;1\lt x\lt 2\;$ and $\;x_Q=9.939535141\;$ for $\;9\lt x\lt 11$ .
- There is a maximum $N$ where the derivative of the argument of the logarithm is zero and
$1/2\lt x\lt 3/2\;$ in $\;2x\, 2^x - 5 x^4 + x^2\,2^x \ln(2) = 0$ .
We find: $(x_N,y_N)=(1.037281920,0.3581062955)$ .
- The vertical asymptotes $A$ and $B$ must be at the zeroes of the argument of the logarithm: $x^2(2^x-x^3)+1=0$ .
We find: $x_A=1.480805180\;$ for $\;1\lt x\lt 2\;$ and $\;x_B=9.939508800\;$ for $\;9\lt x\lt 11$ .
- The slope of the supposed straight line - but is it one? - becomes $\;\ln(2)/\ln(7)\;$ for $\;x \to \infty$ .

