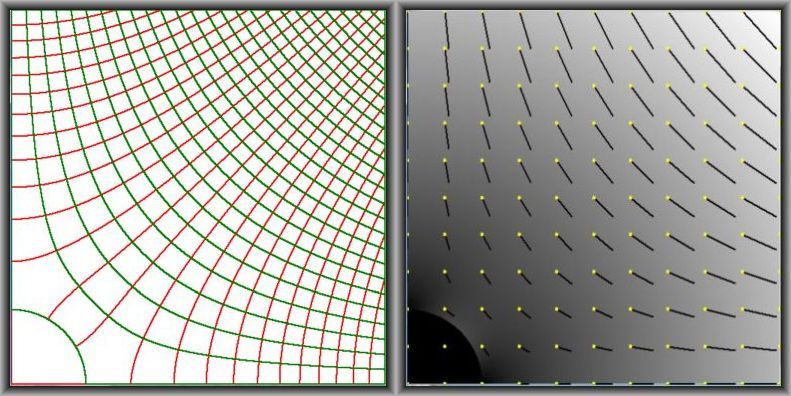

The flow velocities can be calculated as in
this question :
$$
\phi(x,y) = A \left[ x^2-y^2+\frac{x^2-y^2}{(x^2+y^2)^2} \right] \quad \Longrightarrow
$$
$$
u = \frac{\partial \phi}{\partial x} = A \left[ 2 x + \frac{2 x}{(x^2+y^2)^2} - \frac{4(x^2-y^2)x}{(x^2+y^2)^3} \right] \\
v = \frac{\partial \phi}{\partial y} = A \left[ - 2 y - \frac{2 y}{(x^2+y^2)^2} - \frac{4(x^2-y^2)y}{(x^2+y^2)^3} \right]
$$
The speed $\,V=\sqrt{u^2+v^2}\,$ may become a fairly complicated expression in general,
but it is greatly simplified for the boundaries. Let's follow the streamline
with $\psi=0$ from bottom-right to top-left. Then we subsequently have, for the x-axis (with $y=0$ and $v=0$) :
$$
y = 0 \quad , \quad \infty > x \ge 1 \qquad \Longrightarrow \qquad V = 2\,A\frac{x^4-1}{x^3}
$$
for the quarter of a circle (by repeatedly substituting $\,x^2+y^2=1$) :
$$
r=1 \quad , \quad 0 \le \theta \le \pi/2 \qquad \Longrightarrow \qquad
V = 4\,A\,\sqrt{1-(x^2-y^2)^2} = 8\,A\,x\sqrt{1-x^2}
$$
for the y-axis (with $x=0$ and $u=0$) :
$$
x = 0 \quad , \quad 1 \le y < \infty \qquad \Longrightarrow \qquad V = 2\,A\frac{y^4-1}{y^3}
$$
Note that the speed is zero - as well as continuous - for $(x,y)=(1,0)$ and $(x,y)=(0,1)$ .
But .. it's all much easier with polar coordinates.
Flow potential $\phi$ and stream function $\psi$ :
$$
F(z) = A\left[z^2+\frac{1}{z^2}\right]
= A\left[r^2 e^{2i\theta} + \frac{1}{r^2} e^{-2i\theta} \right] \\
= A\left[\left(r^2 + \frac{1}{r^2}\right) \cos(2\theta)\right]
+ i\, A\left[\left(r^2 + \frac{1}{r^2}\right) \sin(2\theta)\right] = \phi + i\,\psi
$$
Flow velocity field $(u,v)$ :
$$
F'(z) = 2 A\left[z - \frac{1}{z^3}\right]
= 2A\left[r e^{i\theta} - \frac{1}{r^3} e^{-3i\theta} \right] \\
= 2A\left[r \cos(\theta) - \frac{1}{r^3}\cos(3\theta)\right]
- i\, 2A\left[- r \sin(\theta) - \frac{1}{r^3}\sin(3\theta)\right] = u - i\, v
$$
Speed $V$ at the boundaries:
$$
\theta = 0 \quad , \quad r > 1 \qquad \Longrightarrow \qquad
V = 2A\left[r - 1/r^3\right] \\
0 \le \theta \le \pi/2 \quad , \quad r = 1 \qquad \Longrightarrow \qquad
V = \left| 2 A \, 2\,i\, e^{- i\theta} \frac{e^{2i\theta} - e^{-2i\theta}}{2\, i}\right|
= 4A\sin(2\theta) \\
\theta = \pi/2 \quad , \quad r > 1 \qquad \Longrightarrow \qquad
V = 2A\left[r - 1/r^3\right]
$$