How find the value of the $x+y$

Viewport:

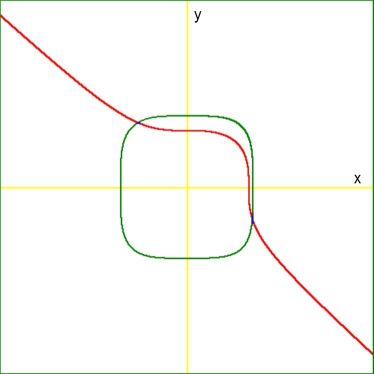
  xmin := -4; xmax := +4;
  ymin := -4; ymax := +4;

EDIT. A parameter representation for the curve $\;3x^3+4y^3=7\;$ is: $$ x(t) = -\sqrt[3]{\frac{t}{3}} \qquad ; \qquad y(t) = \sqrt[3]{\frac{t+7}{4}} $$ This turns the problem into seeking zeroes of a one-dimensional function: $$ f(t) = 4 x^4(t) + 3 y^4(t) - 16 $$ Standard numerical methods can be employed for this purpose. Newton-Raphson and Regula Falsi have been successful here. Our (double precision) results are: $$ t = 3.56874527617414 \quad \Longrightarrow \quad (x,y) = ( -1.05957433921527 , +1.38246606572819 ) \\ t = -8.23503156460535 \quad \Longrightarrow \quad (x,y) = ( +1.40017183631184 , -0.675884813969605 ) $$ Giving, respectively: $$ x+y = 0.322891726512912 \\ x+y = 0.724287022342236 $$ ALGORITHM (Delphi Pascal) :

program RF;

type
  funktie = function(t : double) : double;

function regula_falsi(d1,d0,eps : double; F : funktie) : double;
{
  Regula Falsi
}
var
  OK : boolean;
  d2 : double;
begin
  d2 := d0;
  while abs(F(d2)) > eps do
  begin
    d2 := d1 - F(d1)*(d0 - d1)/(F(d0) - F(d1));
    if F(d2) = 0 then Break;
    OK := (F(d2)*F(d1) < 0);
    if not OK then
    begin
      d1 := d2;
    end else begin
      d0 := d1; d1 := d2;
    end;
    Write(d2,' : ',F(d2),' ; Press Enter'); Readln;
  end;
  regula_falsi := d2;
end;

function power(x,r : double) : double;
var
  M : double;
begin
  M := 0;
  if x > 0 then
    M := exp(r*ln(abs(x)));
  if x < 0 then
    M := -exp(r*ln(abs(x)));
  power := M;
end;

function original(t : double) : double;
{
  Function itself
}
var
  x,y,f : double;
begin
  x := -power(t/3,1/3);
  y :=  power((t+7)/4,1/3);
  f := 4*sqr(sqr(x))+3*sqr(sqr(y))-16;
  original := f
end;

procedure Calculate(x1,x2 : double);
const
  eps : double = 1.E-14;
var
  t,x,y,t1,t2 : double;
begin
  t1 := 3*sqr(x1)*x1;
  t2 := 3*sqr(x2)*x2;
  t := Regula_Falsi(t1,t2,eps,original);
  Writeln(t);
  x := -power(t/3,1/3);
  y :=  power(t/4+7/4,1/3);
  Writeln(x,' +',y,' =',x+y); 
end;

begin
  Calculate( 1.0, 1.5);
  Writeln;
  Calculate(-1.5,-0.5);
end.