How find this equation integer solution: $x^2y^2=4x^5+y^3$

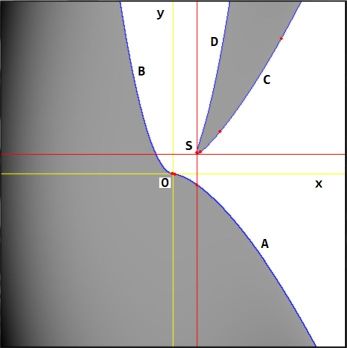
The basic equation is defined here for real $(x,y)$ as well, by: $$ x^2 y^2 = 4 x^5 + y^3 $$ See picture ; window $-200 < x < +200$ , $-4000 < y < +4000$ .
It is immediately clear that $(x,y) = (0,0)$ is an (integer) solution of the equation and that $x = 0 \leftrightarrow y = 0$ . $\color{red}{Tangents}\,$ at the curve are calculated by implicit differentation: $$ 2 x y^2 + x^2 2 y y' = 20 x^4 + 3 y^2 y' \quad \Longrightarrow \quad y' = \frac{20 x^4 - 2 x y^2}{2 y x^2 - 3 y^2} $$ Horizontal tangents at: $$ 20 x^4 - 2 x y^2 = 0 \quad \Longrightarrow \quad y^2 = 10 x^3 $$ Substitute into the basic equation to obtain: $$ x^2 y^2 = 4 x^5 + y^3 \quad \Longrightarrow \quad x^2 \cdot 10 x^3 = 4 x^5 + 10 x^3 y $$ We have covered the trivial solution $(0,0)$ so forget about it in the sequel. $$ 6 x^2 = 10 y \quad \Longrightarrow \quad 36 x^4 = 100 y^2 = 1000 x^3 \quad \Longrightarrow \quad (x_S,y_S) = \left(\frac{10^3}{6^2},\sqrt{\frac{10^{10}}{6^6}}\right) $$ The Special point  S  is important for the numerical work that follows. Vertical tangents at: $$ 2 y x^2 - 3 y^2 = 0 \quad \Longrightarrow \quad y = \frac{2}{3} x^2 $$ Substitute into the basic equation to obtain: $$ x^2 \cdot \frac{4}{9} x^4 = 4 x^5 + \frac{8}{27} x^6 \quad \Longrightarrow \quad \frac{4}{27} x = 4 \quad \Longrightarrow \quad (x,y) = (27,486) $$ The latter happens to be one of the required integer solutions !
The rest of the method is brute force.
It is clear from the picture that there are four branches:

• one extending from $(0,0)$ towards minus infinity in the quadrant $x > 0$ , $y < 0$
  indicated as A
• one extending from $(0,0)$ towards plus infinity in the quadrant $x < 0$ , $y > 0$
  indicated as B
• one extending from the special point  S  towards plus infinity on the right side
  in the quadrant $x > 0$ , $y > 0$ , indicated as C
• one extending from the special point  S  towards plus infinity on the left side
  in the quadrant $x > 0$ , $y > 0$ , indicated as D

program krabbel;

function pow(x : double; n : integer) : double;
var
  q : double;
  k : integer;
begin
  q := 1;
  for k := 1 to n do
    q := q * x;
  pow := q;
end;

function f(x,y : double) : double;
begin
  f := pow(x,2)*pow(y,2) - (4*pow(x,5) + pow(y,3));
end;

procedure crawl_A;
var
  x,y : integer;
  g : double;
begin
  x := 0; y := 0;
  while true do
  begin
    y := y - 1;
    g := f(x,y);
    if g = 0 then Writeln(x,' ',y);
    while g > 0 do
    begin
      x := x + 1;
      g := f(x,y);
      if g = 0 then Writeln(x,' ',y);
    end;
  end;
end;

procedure crawl_B;
var
  x,y : integer;
  g : double;
begin
  x := 0; y := 0;
  while true do
  begin
    y := y + 1;
    g := f(x,y);
    if g = 0 then Writeln(x,' ',y);
    while g < 0 do
    begin
      x := x - 1;
      g := f(x,y);
      if g = 0 then Writeln(x,' ',y);
    end;
  end;
end;

procedure crawl_C;
var
  x,y : integer;
  g : double;
begin
  x := Round(pow(10,3)/pow(6,2));
  y := Round(sqrt(pow(10,10)/pow(6,6)));
  while true do
  begin
    y := y + 1;
    g := f(x,y);
    if g = 0 then Writeln(x,' ',y);
    while g > 0 do
    begin
      x := x + 1;
      g := f(x,y);
      if g = 0 then Writeln(x,' ',y);
    end;
  end;
end;

procedure crawl_D;
var
  x,y : integer;
  g : double;
begin
  x := 27; y := 486;
  while true do
  begin
    y := y + 1;
    g := f(x,y);
    if g = 0 then Writeln(x,' ',y);
    while g < 0 do
    begin
      x := x + 1;
      g := f(x,y);
      if g = 0 then Writeln(x,' ',y);
    end;
  end;
end;

begin
{ crawl_A; crawl_B; } crawl_C; { crawl_D; }
end.

Results $\;\rightarrow picture: \color{red}{dots}$

by hand:
0 0
27 486

crawl_A:
2 -4
27 -243

crawl_B:
-1 2

crawl_C:
32 512
54 972
125 3125

crawl_D:
nothing