This is again a question of the symmetric type, such as listed in:
With a constraint $\;x+y+z=1\;$ and $\;x,y,z > 0$ .
Sort of a general method to transform such a constraint into the inside of a triangle in 2-D has been explained at length in:
The above preliminaries are completed with:
From the latter article comes the following
Theorem (The Purkiss Principle). Let $f$ and $g$ be symmetric functions with continuous second derivatives
in the neighborhood of a point $P = (r, \cdots, r)$. On the set where $g$ equals $g(P)$, the function $f$ will have
a local maximum or minimum at $P$ except in degenerate cases.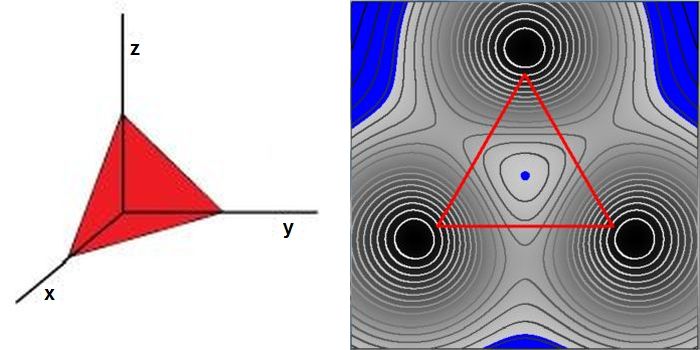
- Picture on the left: geometry of the conditions $\;x,y,z > 0\;$ and $\;x+y+z=1$ .
- Picture on the right: contour lines of $f(x,y,z)$ , as seen in the plane of the $\color{red}{red}$ triangle,
are at $20$ equidistant levels, between the minimum and the maximum as found within the viewport
Our function $f$ in this case is:
$$ f(x,y,z) = \frac{x}{3y^2+3z^2+3yz+1}+\frac{y}{3x^2+3z^2+3xz+1}+\frac{z}{3x^2+3y^2+3xy+1} $$
Applying the Purkiss Principle gives:
$$ g(r,r,r)=r+r+r=1 \quad \Longrightarrow \quad r=\frac{1}{3} \quad \Longrightarrow \quad f(r,r,r) = \frac{1}{2} $$
The main problem with the Purkiss Principle, most of the time, is to prove that the extreme found is global.
Or at least global enough , i.e. an absolute extreme inside our ($\color{red}{red}$) triangle.
In our case, the function will become less than $1/2$, namely close to zero, for $\;|x|,|y|,|z|\rightarrow \infty$ .
So it's clear that the Purkiss Principle is "violated", outside the triangle at least.
These regions, where $\;f(x,y,z)\;$ is less than, say, $1/2 + 0.001$ , are colored $\color{blue}{blue}$ in the picture on the right.
The $\color{blue}{blue\, spot}$ in the picture on the right is a proof without words that the only minimum inside the triangle
is (indeed $= 1/2$ ) and at its center $(x,y,z) = (1/3,1/3,1/3)$ . This finishing touch is thus an informal proof (: disclaimer).
Update : a few further details.
- Function values close to viewport minimum are white
- Function values close to viewport maximum are black
- Contour grey values are just the other way around
- Function values at the corners of the triangle $=1$ (black)
- Function values at the edge centers of the triangle $=4/7$

