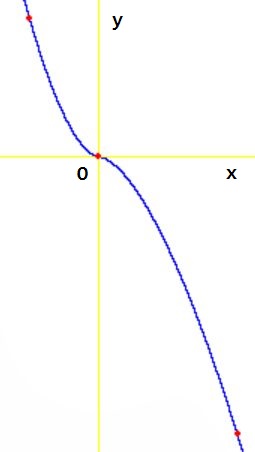
What is the slope of the tangent at $(0,0)$ on the curve $x^2y^2=4x^5+y^3$

This question is arising from the answer to another one: How find this equation integer solution: $x^2y^2=4x^5+y^3$ . For $x < 27$ and $y > -243$ , the basic equation $x^2 y^2 = 4 x^5 + y^3$ is a function. By implicit differentiation we have found that: $$ y'(x) = \frac{20 x^4 - 2 x y^2}{2 y x^2 - 3 y^2} \quad \Longrightarrow \quad y'(0) = \; ? $$ From the picture it is suspected that: $y'(0) = 0$ , i.e. the slope of the tangent in $(x,y) = (0,0)$ may be zero. But I could not prove or disprove it. Any ideas?

Update.
When solving for $y$ (with help of MAPLE) we find something that looks like a decent function, within a prescribed range e.g. $-1 < x < +2$ ; see picture. (Bonus: integer solutions original question at red spots) $$ y(x) = \left[\frac{\left(-54 x^2 + x^3 + 6 \sqrt{81 x^4 - 3 x^5}\right)^{1/3}}{3} + \frac{x^2}{3\left(-54 x^2 + x^3 + 6 \sqrt{81 x^4 - 3 x^5}\right)^{1/3}} + \frac{x}{3}\right] x $$ So it's still not clear to me why the derivative $y'(0)$ would be somehow undefined.

   

A rather extreme close-up , namely $-1/10 < x < 1/10$ : picture on the right , doesn't reveal any other slope than zero at $(0,0)$ . Whiter means that the function $f(x,y) = 4 x^5 + y^3 - x^2 y^2\;$ is closer to zero; it is seen that $\;f(x,y)\;$ is very close to zero indeed in the neighborhood of $(0,0)$ , thus suggesting that the tangent may be ambiguous there. But is it?

My try.   Draw a circle with radius $r > 0$ and $(0,0)$ as its midpoint: $$ x = r \cos(\phi) \qquad y = r \sin(\phi) $$ Substitute this into the basic equation $\;x^2 y ^2 = 4 x^5 + y^3\;$ and divide by $r^3$ : $$ 4 \cos^5(\phi)\, r^2 - \cos^2(\phi) \sin^2(\phi)\, r + \sin^3(\phi) = 0 $$ If $\;r \rightarrow 0\;$ i.e. becomes very small, then function values in the neighborhood of $\;(0,0)\;$ only depend on the last term $\;\sin^3(\phi)$ . Meaning that $\phi \approx 0$ or $\phi \approx \pi$ . The tangent through these two points has slope zero. Don't know if this counts as a proof.

The clue of this answer is actually given by David Speyer so I shall give him the credit. What follows is for the sake of completeness and clarity. $$ x(t) = \frac{t^3}{(4-t)^2} \qquad , \qquad y(t) = -\frac{t^5}{(4-t)^3} \qquad \Longrightarrow \\ x'(t) = \frac{t^2\,(12-t)}{(4-t)^3} \qquad , \qquad y'(t) = -\frac{2\,t^4\,(10-t)}{(4-t)^4} \qquad \Longrightarrow \\ \frac{dy}{dx} = \frac{y'(t)}{x'(t)} = -\frac{2\,t^2\,(10-t)}{(12-t)(4-t)} \qquad \Longrightarrow \qquad \lim_{t\rightarrow 0} \frac{y'(t)}{x'(t)} = 0 = \frac{dy}{dx}(0,0) $$ It's not necessary to use a computer algebra system for this (though I used it as well :-).
Anyway, herewith the proof is complete.
$$ x^2y^2 = \left[\frac{t^3}{(4-t)^2}\right]^2\left[-\frac{t^5}{(4-t)^3}\right]^2=\frac{t^{16}}{(4-t)^{10}} \\ 4x^5+y^3 = 4\left[\frac{t^3}{(4-t)^2}\right]^5+\left[-\frac{t^5}{(4-t)^3}\right]^3 = \frac{4t^{15}-t^{15}(4-t)}{(4-t)^{10}}=\frac{t^{16}}{(4-t)^{10}} $$