Several examples that use skew coordinates, questions & answers all very similar:
This is the reference that describes the transformation:
The main result is repeated here for convenience:
$$
\left[ \begin{array}{c} x - x_1 \\ y - y_1 \end{array} \right] =
\left[ \begin{array}{cc} (x_2 - x_1) & (x_3 - x_1) \\
(y_2 - y_1) & (y_3 - y_1)
\end{array} \right]
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right]
$$
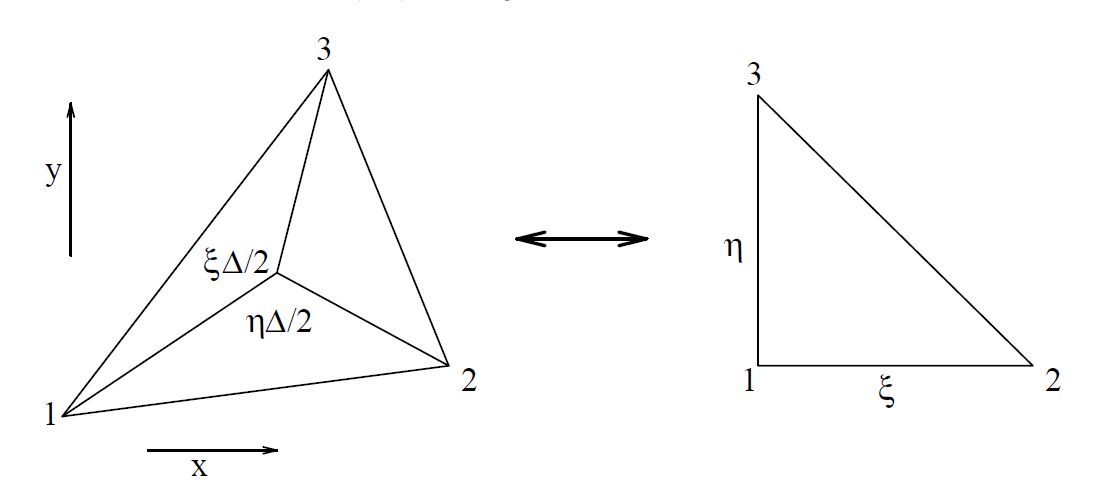
Note that the triangle is half a parallelogram. And instead of
transforming a parallelogram into a rectangle, an arbitrary triangle is
transformed into a rectangular isosceles triangle. Therefore the above is in fact equivalent
with any skew linear transformation (+ translation) :
$$
\left[ \begin{array}{c} x \\ y \end{array} \right] =
\left[ \begin{array}{cc} \alpha & \beta \\
\gamma & \delta
\end{array} \right]
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right]
+ \left[ \begin{array}{c} p \\ q \end{array} \right]
$$
If we define the coordinates of our transformed triangle as:
$\,(x_1,y_1) = (p,q)\,$ , $\,x_2 = \alpha + p\,$ , $\,x_3 = \beta + p\,$ ,
$\,y_2 = \gamma + q\,$ , $\,y_3 = \delta + q\,$.
Note. Via Finite Element interpolations, other parent polytopes
are associated with non-linear transformations. For example the standard
quadrilateral with vertices
$(1)=(-1,-1)\, ,\, (2)=(+1,-1)\, ,\, (3)=(-1,+1)\, ,\, (4)=(+1,+1)\,$ has bilinear interpolation:
$$
f = \frac{1}{4}(1-\xi)(1-\eta)f_1
+ \frac{1}{4}(1+\xi)(1-\eta)f_2
+ \frac{1}{4}(1-\xi)(1+\eta)f_3
+ \frac{1}{4}(1+\xi)(1+\eta)f_4 \\
= \sum_{k=1}^4 N_k(\xi,\eta)\,f_k \qquad \mbox{with} \qquad N_k(\xi,\eta) = \frac{1}{4}(1\pm\xi)(1\pm\eta)
$$
The accompanying (isoparametric) transformation is found by replacing $f$ with
$x$ and $y$ :
$$
x = \sum_{k=1}^4 N_k(\xi,\eta)\,x_k \qquad ;
\qquad y = \sum_{k=1}^4 N_k(\xi,\eta)\,y_k
$$
The bilinear transformation becomes linear again if the quadrilateral is a
parallelogram ,
because then $\,x_1+x_4=x_2+x_3\,$ and $\,y_1+y_4=y_2+y_3\,$ (: diagonals property) , as substituted in:
$$
f = (f_1+f_2+f_3+f_4)/4 + \xi\,(-f_1+f_2-f_3+f_4)/4 + \eta
\, (-f_1-f_2+f_3+f_4)/4 \\
+ \xi\eta\,(f_1-f_2-f_3+f_4)
$$
and hence the last term becomes zero.

