Evaluate $\int_0^{\pi/2} \frac{\ln\left(e^{2x} + 1\right)}{1 + \sin2x}\mathrm dx$

The OP asked for an answer using numerical analysis. Let me first say that even Mathematica and MAPLE do not give exactly the same answers for this integral. MAPLE gives: 
F(x) := ln(exp(2*x)+1)/(1+sin(2*x));
evalf(int(F(x),x=0..Pi/2),16);
                                              1.830481056481415
As compared with the value in the comment by Iuʇǝƃɹɐʇoɹ : $1.830481056481482$ .
Then OK, here is a very brute force (and therefore a piece of cake) program: 
program numeric;

function F(x : double) : double;
begin
  F := ln(exp(2*x)+1)/(1+sin(2*x));
end;

function lower(N : integer) : double;
var
  k : integer;
  x,dx,sum : double;
begin
  sum := 0;
  dx := (Pi/2)/N;
  for k := 0 to N-1 do
  begin
    x := (Pi/2)*k/N+dx/2;
  { Midpoint rule }
    sum := sum + F(x)*dx;
  end;
  lower := sum;
end;

function upper(N : integer) : double;
var
  k : integer;
  x1,x2,dx,sum : double;
begin
  sum := 0;
  dx := (Pi/2)/N;
  x2 := 0;
  for k := 1 to N do
  begin
    x1 := x2;
    x2 := (Pi/2)*k/N;
  { Trapezium rule }
    sum := sum + (F(x1)+F(x2))/2*dx;
  end;
  upper := sum;
end;

begin
  Writeln(lower(1000000));
  Writeln(upper(1000000));
end.
Output: 
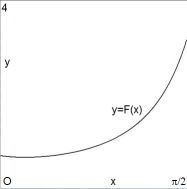
 1.83048105648054E+0000
 1.83048105648321E+0000
It helps to make a little sketch of the function $F(x) = \ln(e^{2x}+1)/(1+\sin(2x))$ :

Due to this function behaviour, the Midpoint rule give a lower bound, while the Trapezium rule gives an upper bound for the integral. Thus we find with certainty that: $$ 1.830481056480 < \int_{0}^{\pi/2} \frac{\ln\left(e^{2x} + 1\right)}{1 + \sin2x}\mathrm dx < 1.830481056484 $$ The results with Mathematica and MAPLE are well within these bounds.