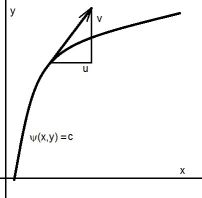

Thus, along the curve $\psi(x,y) = c$ , the following equations hold: $$ \left. \begin{array}{l} \frac{dy}{dx} = \frac{v}{u} \\ d\psi = 0 = \frac{\partial \psi}{\partial x} dx + \frac{\partial \psi}{\partial y} dy \end{array} \right\} \qquad \Longrightarrow \qquad \frac{dy}{dx} = - \frac{\partial \psi / \partial x}{\partial \psi / \partial y} = \frac{v}{u} $$ Hence, apart from a constant: $$ u = \frac{\partial \psi}{\partial y} \qquad ; \qquad v = - \frac{\partial \psi}{\partial x} $$ But the flow is incompressible, so: $$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 \qquad \Longrightarrow \qquad \frac{\partial^2 \psi}{\partial x\, \partial y} = \frac{\partial^2 \psi}{\partial y\, \partial x} $$ Herewith the conditions for an exact differential equation are fulfilled. Now solve $\psi$ from: $$ v\, dx - u\, dy = 0 $$ Example. As taken from : Find the velocity of a flow . $$ u = -\frac{y}{x^2+y^2} \qquad ; \qquad v = \frac{x}{x^2+y^2} $$ Then: $$ v\, dx - u\, dy = \frac{x\,dx + y\,dy}{x^2+y^2} = \frac{d\left( x^2+y^2 \right)}{x^2+y^2} = 0 \qquad \Longrightarrow \qquad x^2 + y^2 = c $$ It is concluded that the streamlines of this flow are circles.
Example. Somewhat related to the above one. $$ u = \lambda\,x \qquad ; \qquad v = \lambda\,y $$ Then, assuming that $\; x\ne 0$ (i.e. $\,x=0\,$ as a special case) : $$ v\, dx - u\, dy = 0 \quad \Longleftrightarrow \quad \frac{y\,dx - x\,dy}{x^2} = - d(y/x) = 0 \quad \Longrightarrow \quad y = c\, x $$ An integrating factor has been used. It is concluded that the streamlines of this flow are straight lines through the origin.
Wikipedia reference:
The electric potential at a point $\vec{r}$ in a two-dimensional static electric field $\vec{E}$ is given by the line integral: $$ V = - \int_C \vec{E}\cdot d\vec{r} = - \int_C \left(E_x\, dx + E_y\, dy\right) $$ where $C$ is an arbitrary path connecting the point with zero potential to $\vec{r}$. It follows that: $$ E_x = - \frac{\partial V}{\partial x} \qquad ; \qquad E_y = - \frac{\partial V}{\partial y} $$ The integral is zero if the path is closed. Then Green's theorem tells us: $$ \oint \left( E_x\, dx + E_y\, dy \right) = \iint \left( \frac{\partial E_y}{\partial x} - \frac{\partial E_x}{\partial y} \right) dx\,dy = - \iint \left( \frac{\partial^2 V}{\partial x \, \partial y} - \frac{\partial^2 V}{\partial y \, \partial x}\right) dx\,dy = 0 $$ Thus establishing once more the conditions for solvability of the exact differential equation: $$ E_x \, dx + E_y \, dy = 0 $$ Solving this ODE results in the iso-lines $\,V(x,y) = c\,$ of the electric potential $\,V$ .
Example. An infinitely long and infinitely thin
charged wire perpendicular to the plane and intersecting it
in the origin. Apart from constants:
$$
(E_x,E_y) = \frac{(x,y)}{r^2} \quad \Longrightarrow \quad
E_x\, dx + E_y\, dy = \frac{x\,dx + y\,dy}{r^2} = 0
\quad \Longrightarrow \quad x^2+y^2 = c
$$
The equipotential lines are circles.
Can of worms: special cases, and a singularity at the origin in all of the examples.