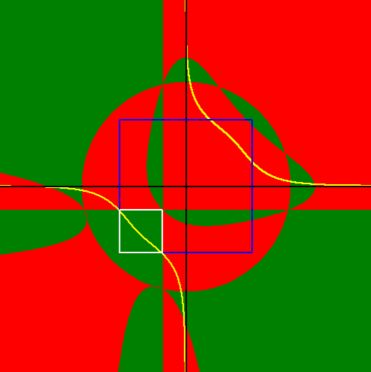

Mind the circle and the straight lines; they are the singularities in the function $P(x,y)$ . Also note that the whole problem has a mirror symmetry with respect to the line $\;y=x$ . Our viewport is:
xmin := -4; xmax := +4; ymin := -4; ymax := +4;First investigate where $P$ is positive ($\color{red}{red}$) and where it is negative ($\color{green}{green}$) . We seek a minimum, so attention will be preferably be restricted to the domains where $P(x,y)$ is $\color{green}{negative}$. Then define the curve (yellow in the picture). The minimum of $P(x,y)$ must be at this curve $C$ : $$ x^4+y^4+4=\dfrac{6}{xy} \qquad \mbox{or} \qquad C(x,y) = xy \, (x^4+y^4+4)-6=0 $$ The coordinate axes are in black, the area $\;x,y\in (-\sqrt2;\sqrt2)\;$ to be investigated is the square enclosed by the $\color{blue}{blue}$ lines. Now it is immediately clear that the domain to be investigated in the end is the one enclosed by the white borders: $\;x,y\in (-\sqrt2;-1/2)$ . The white bordered part of the picture is enlarged here:
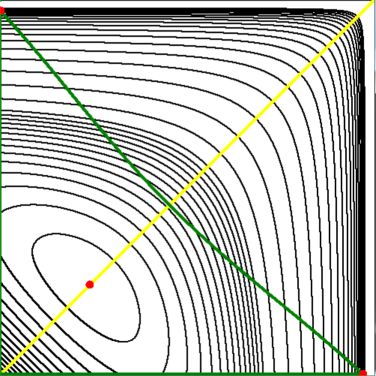
Some contour lines of the function $P(x,y)$ are drawn in black; the curve
$C(x,y) = 0$ is drawn in $\color{green}{green}$. The line of symmetry $y=x$
is colored yellow; extrema of the function $P(x,y)$ are marked with
$\color{red}{red}$ colored dots. A special place is the maximum of $P$ at
the curve $\,C=0$ , the intersection point of the green and the yellow line :
$$
C(-1,-1) = 0 \qquad \mbox{and} \qquad P(-1,-1) = -\frac{5}{3}
$$
The curve $\;C(x,y)=0\;$ intersects the lines $\;x=-\sqrt{2}\;$
and $\;y-\sqrt{2}\;$ just below $\;y=-1/2\;$ and left of $\;x=-1/2\;$ , because
these points are in the negative zone of the function $\;C(x,y)$ :
$$
C(-\sqrt{2},-1/2) = C(-1/2,-\sqrt{2}) = \frac{129}{16}-6\sqrt{2} = -.422781372 < 0
$$
A local maximum ( $\color{red}{red \; dot}$ ) has been detected (but only)
numerically:
$$
P(-1.194436916,-1.194436916) = -1.371703810
$$
Last but not least: the minimum value that is asked for. Because the interval
$(-\sqrt2;\sqrt2)$ is defined by the OP as an open interval (?) , that's a
tricky one. If the interval were closed, then I would say the two minima are
at the solutions of $\;C(-\sqrt{2},y)=0\;$ or $\;C(x,-\sqrt{2})=0\;$ :
$$
y^5 + 8y + 3 \sqrt{2} = 0 \qquad \mbox{or} \qquad x^5 + 8x + 3 \sqrt{2} = 0
$$
A quintic which can be solved (only?) numerically : $\;y = -.5253289716 < -1/2$
or $\;x = -.5253289716 < -1/2$ .
The minimum itself is (numerically) :
$$
P(-\sqrt{2},-.5253289716) = P(-.5253289716,-\sqrt{2}) = -19.73131147
$$
But I don't know how to properly handle the open interval, if it is meant as such.
$P(x,y)\;$ along the curve $\;C(x,y) = 0\;$ inside $\;x,y \in (-\sqrt2;-1/2)\;$
is a function $\;y = f(s)\;$ where $\;s\;$ is the arc length. We can plot the graph
of $\;y=f(s)$ . Due to the symmetry, it doesn't matter in which direction we
walk along the curve. It is seen that the maximum is indeed at $\;y=-5/3\;$ and
that the function is uniformly descending from there in both (symmetric) directions.
