Relevant questions and answers, in chronological order:
All of the questions and answers are related to the
Moment problem .
The functions considered have compact support (hope this terminology is correct).
More specifically, the above Q & A list is related to the
Hausdorff moment problem ;
without loss of generality, the bounded interval is taken as $[0,1]$ .
As pointed out in the Wikipedia reference, the following integral sheds more light
on properties of the moments. Let $f(x)$ be real, integrable and positive with area
$\,m_0 = 1\,$ equal to one - in short: $f(x)$ resembles a Probability Density Function (PDF) - then:
$$
\int_0^1 f(x) x^n (1-x)^k dx > 0 \quad \Longrightarrow \quad \left\{
\begin{array}{l} m_0 > 0 \; , \; m_1 > 0 \; , \; m_2 > 0 \\
m_0 > m_1 \; , \; m_2 > m_1 \\
m_0 - 2 m_1 + m_2 > 0 \end{array}\right.
$$
Attention will be restricted to the first few moments : $m_1,m_2$ .
If we put $\;x = m_1/m_0=m_1\;$ and $\;y = m_2/m_0=m_2\;$ then it follows that all $(x,y)$
values are within the $\color{silver}{silver}$ triangle with vertices
$(0,0),(0,1/2),(1,1)$ , as shown in the picture at the bottom.
$$
y > 0 \quad ; \quad y < x \quad ; \quad y > 2 x - 1
$$
Schwarz' inequality gives rise to a somewhat more restrictive condition: all $(x,y)$
values are within the $\color{gray}{gray}$ area between a parabola and a straight line:
$$
y < x \quad ; \quad y > x^2
$$
This is as far as I have been able to go with general considerations about moments.
But if someone knows better, I'm eager to learn about it.
Special theories
Couldn't proceed with the general, so I've tried some special cases. Because I think it's better to be successful
with something special than to fail with anything general. This is the reason why I've
payed so much attention to extremely simple PDF-functions, sample functions namely that
are completely determined by their first few moments. Among these are:
-
histograms consisting of three blocks with the same width
Please read the reference, because the argumentation shall not repeated here.
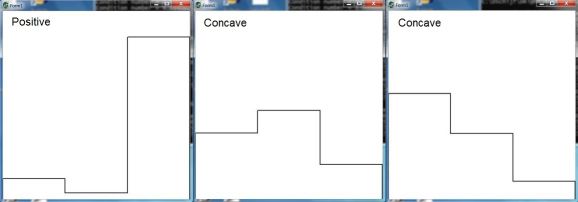
The three moments $\,m_0,m_1,m_2\,$ are linear in the three function values
$f_0,f_1,f_2$ and vice versa. Meaning that there is a one-to-one mapping between
function space and moment space $\,(x=m_1/m_0,y=m_2/m_0)\,$ where $m_0 = 1$ .
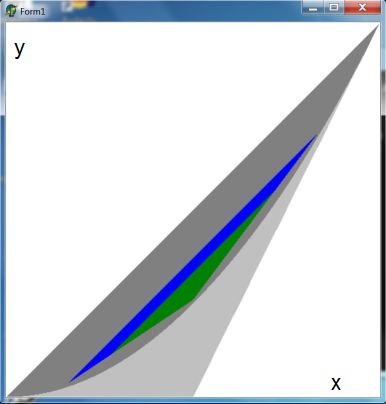
The moment space of 3-histograms is in the picture below. If the only
requirement is that the histogram is just positive (and with area $= 1$) then
what we have is the $\color{blue}{blue\; triangle}$. If an additional requirement
is that the histogram is concave then we have the $\color{green}{green\; triangle}$
as a proper part of the blue one. Let's formulate this as follows.
Consider the
universe of all PDF 3-histograms, what then is the chance that such a histogram
is concave ? The answer must be the quotient of the areas of
the green and the blue triangle. With the above reference that is: $\,(4/243) / (1/27) = 4/9$ .
With other words: $\large 4/9$ of all histograms in our special universe are concave.
 !
!
But this is indeed a very simple example. A couple of questions arise:
-
In general, has an idea like this been launched before?
-
If not in general, do there exist other special examples of PDF universes
where the question "what is the chance that a PDF is concave" makes sense?
There is another example in the abovementioned
special answer
which is less complete there and shall
be completed here.
Consider the universe of all PDF-like parabolic functions
at the interval $t \in [0,1]$ :
$$
p(t) = a_0 + a_1 t + a_2 t^2
$$
The following Q & A has been helpful with visualization of the parabolas:
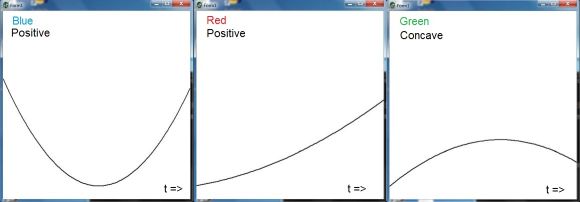
There is a linear relationship between the coefficients
of the parabola and the first few moments, via the Hilbert matrix and its inverse:
$$
\left[ \begin{array}{c} m_0 \\ m_1 \\ m_2 \end{array} \right] =
\left[ \begin{array}{ccc} 1 & 1/2 & 1/3 \\ 1/2 & 1/3 & 1/4 \\ 1/3 & 1/4 & 1/5 \end{array} \right]
\left[ \begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right] \quad \Longleftrightarrow \quad
\left[ \begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right] =
\left[ \begin{array}{ccc} 9 & -36 & 30 \\ -36 & 192 & -180 \\ 30 & -180 & 180 \end{array} \right]
\left[ \begin{array}{c} m_0 \\ m_1 \\ m_2 \end{array} \right]
$$
As usual, we define the coordinates in moment space as $\,x=m_1/m_0\,$ and $\,y=m_2/m_0\,$
with the area normed to one $\,m_0=1$ .
Let's start with demanding that the parabolas are positive at $[0,1]$ .
Which is e.g. the case if the discriminant is negative together with a positive leading coefficient:
$$\color{blue}{
\left. \begin{array}{l} a_1^2 - 4 a_2 a_0 < 0 \\ a_2 > 0 \end{array} \right\}
\quad \Longleftrightarrow \quad \left\{ \begin{array}{l}
152 x^2 - 300 x y + 150 y^2 - 42 x + 40 y + 3 < 0 \\
y - x + 1/6 > 0 \end{array} \right. }
$$
Note that what's up here is exactly (the inside of) the ellipse that was questioned about in:
with the line $y - x + 1/6 = 0$ tangent to it in $B=(1/2,1/3)$ .
This question and
its answers are a prerequisite for understanding what follows.
Another way for the parabola to be positive is that $\;p(0) > 0\;$ and $\;p'(0) > 0\;$ ,
or $\;p(1) > 0\;$ and $\;p'(1) < 0\;$ , again with positive $a_2$ :
$$ \color{red}{
\left. \begin{array}{l} a_0 > 0 \\ a_1 > 0 \\ a_2 > 0 \end{array} \right\}
\quad \Longleftrightarrow \quad \left\{ \begin{array}{l}
y - 6/5 x + 3/10 > 0 \\
y - 16/15 x + 1/5 < 0 \\
y - x + 1/6 > 0 \end{array} \right. }
$$
$$ \color{red}{
\left. \begin{array}{l} a_0+a_1+a_2 > 0 \\ 2a_2+a_1 < 0 \\ a_2 > 0 \end{array} \right\}
\quad \Longleftrightarrow \quad \left\{ \begin{array}{l}
y - 4/5 x + 1/10 > 0 \\
y - 14/15 x + 2/15 < 0 \\
y - x + 1/6 > 0 \end{array} \right. }
$$
At last we have the possibility that the parabola is concave and positive:
$$ \color{green}{
\left. \begin{array}{l} a_0 > 0 \\ a_0+a_1+a_2 > 0 \\ a_2 < 0 \end{array} \right\}
\quad \Longleftrightarrow \quad \left\{ \begin{array}{l}
y - 6/5 x + 3/10 > 0 \\
y - 4/5 x + 1/10 > 0 \\
y - x + 1/6 < 0 \end{array} \right. }
$$
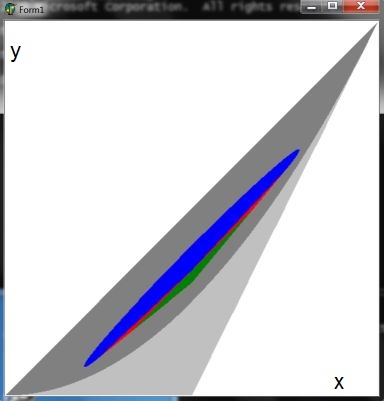
Working out the data results in the "ellipse with a hat" geometry
as has been presented before.
Now we are ready to answer the question: what is the probability that a parabolic PDF at $[0,1]$ is concave ?
The answer is the area of the $\color{green}{green}$ triangle in the picture below divided by the
area of the ellipse-with-a-hat as a whole (i.e. $\color{blue}{blue} + \color{red}{red} + \color{green}{green}$ ).
And the end result is:
$$
\frac{1/180}{\pi\sqrt{3}/180(1-1/3)+1/120+2/720+1/180} = \frac{1}{2\pi/\sqrt{3}+3}
\approx 15 \%
$$
If I am allowed to say something subjective: I find the
geometry associated with this very specific problem of
an astonishing beauty. It all fits so neatly together
that it's almost a miracle.


 !
!

