An ellipse is given by the following equation:
$$
152 x^2 - 300 x y + 150 y^2 - 42 x + 40 y + 3 = 0
$$
After solving for the midpoint we have:
$$
152 (x-1/2)^2 - 300 (x-1/2) (y-11/30) + 150 (y-11/30)^2 = 1/6
$$
Introducing polar coordinates:
$$
x = 1/2 + r \cos(\theta) \quad ; \quad y = 11/30 + r \sin(\theta)
$$
Giving:
$$
152\, r^2 \cos^2(\theta) - 300\, r^2\, \cos(\theta) \sin(\theta) +
150\, r^2 \sin^2(\theta) = 1/6 \quad \Longrightarrow \\
\frac{1}{2} r^2(\theta) = \frac{1/12}
{152 \cos^2(\theta) - 300 \cos(\theta) \sin(\theta) + 150 \sin^2(\theta)}
$$
The area of a sector of the ellipse is:
$$
\int_{\theta_1}^{\theta_2} \frac{1}{2} r^2(\theta) \, d\theta
$$
So it seems that we have to find the indefinite integral:
$$
\int \frac{1/12 \, d\theta}
{152 \cos^2(\theta) - 300 \cos(\theta) \sin(\theta) + 150 \sin^2(\theta)}
$$
And then I'm stuck. Because feeding this into MAPLE with
int(1/12/(152*cos(theta)^2-300*cos(theta)*sin(theta)+150*sin(theta)^2),theta);
quite to my surprise, gives a complex result:
$$
{\frac {1}{720}}\,i\sqrt {3}\ln \left( \left( \tan \left( 1/2\,\theta
\right) \right) ^{2}+ \left( {\frac {5}{38}}\,i\sqrt {3}+{\frac {75}
{38}} \right) \tan \left( 1/2\,\theta \right) -1 \right) \\ -{\frac {1}{720
}}\,i\sqrt {3}\ln \left( \left( \tan \left( 1/2\,\theta \right)
\right) ^{2}+ \left( -{\frac {5}{38}}\,i\sqrt {3}+{\frac {75}{38}}
\right) \tan \left( 1/2\,\theta \right) -1 \right)
$$
But I'm pretty sure that the area of an ellipse sector is a real number.
So the question is: does there exist a closed form for the abovementioned
integral that is real valued instead of complex? What is it? And why that complex result with MAPLE?
AfterMath (see accepted answer)
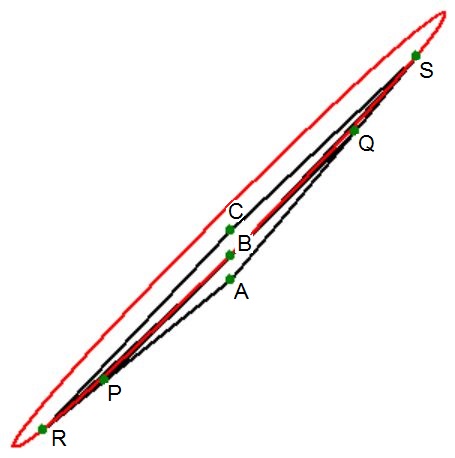$$
A = (1/2,3/10) \quad ; \quad B = (1/2,1/3) \quad ; \quad C = (1/2,11/30) \\
P = (1/3,1/6) \quad ; \quad Q = (2/3,1/2) \\
R = (1/4,1/10) \quad ; \quad S = (3/4,3/5)
$$
Triangle edges are black; ellipse is $\color{red}{red}$ .
Triangle areas:
$\Delta PAQ = 1/180$ , $\Delta PRB = \Delta QSB = 1/720$ .
It is conjectured that the ellipse sector area $\overline{CRBSC}$
is exactly $1/3$ of the total ellipse area;
the latter being
$ = \pi\sqrt{3}/180$ . Can someone prove or disprove this conjecture?
The integral is elementary.
$$
I = \int \frac{d \theta}
{a \cos^2(\theta) - b \cos(\theta) \sin(\theta) + c \sin^2(\theta)}=
\int \frac{d \tan(\theta)}
{a - b \tan(\theta) + c \tan^2(\theta)}
$$
Let $u=\tan(\theta)$ , then:
$$
I = \int \frac{d u}{c u^2 - b u + a} =
\int \frac{d u/c}{\left[ u-b/(2c) \right]^2+a/c - \left[b/(2c)\right]^2}=\\
2 \int \frac{d (2c u-b)}{(2c u-b)^2+(4ac-b^2)}=
\frac{2}{\sqrt{4ac-b^2}} \int \frac{d\left[(2c u-b)/ \sqrt{4ac-b^2}\right]}
{1+\left[(2c u-b)/\sqrt{4ac-b^2}\right]^2}
$$
Now let $\Delta = \sqrt{4ac-b^2}$ and we're finished:
$$
I(\;\tan(\theta)\;) =
\frac{2}{\Delta} \arctan\left(\frac{2c\tan(\theta)-b}{\Delta}\right)
$$
Fill in the numbers for our sector: $a = 152\;,\;b = 300\;,\;c = 150$ ,
$\tan(\theta_2) = 16/15\;,\;\tan(\theta_1) = 14/15$ ; remember that an
$\arctan$ is only defined for arguments $\in \left[-\pi/2,+\pi/2\right]$
and that the whole area of the ellipse equals $\pi\sqrt{3}/180$ . Then:
$$
\mbox{area} = \frac{\pi\sqrt{3}}{180}/2 - \left[\;I(16/15)-I(14/15)\;\right]/12 =
\frac{\pi\sqrt{3}}{540}
$$
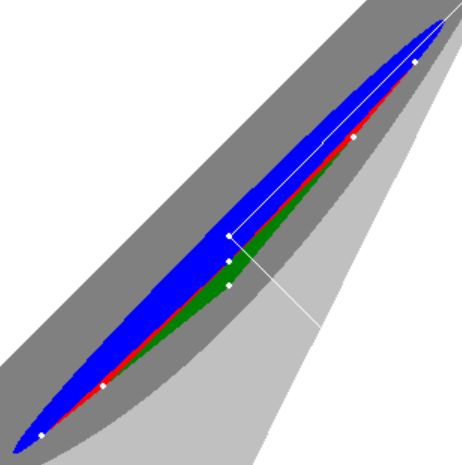
Thus establishing that the AfterMath conjecture is true. So finally we have all the ingredients to calculate the area of
the "ellipse with a hat" ( $\color{blue}{blue} + \color{red}{red} + \color{green}{green}$ ) :
$$
\color{blue}{\pi\sqrt{3}/180(1-1/3)+1/120}+\color{red}{2/720}+\color{green}{1/180} =
\frac{\pi\sqrt{3}}{270}+\frac{1}{60}
$$
