The area of the region $|x-ay| \le c$ for $0 \le x \le 1$ and $0 \le y \le 1$

All sub cases. Consider the strip embedded inside the square, as mentioned in the question, a bit modified though (without loss of generality): $$ \left|\, \cos(\phi) x + \sin(\phi) y\, \right| < c \quad \mbox{with} \; c > 0 \; , \; 0 \le \phi < \pi \quad \mbox{for} \; 0 \le x \le 1 \; , \; 0 \le y \le 1 $$ The vertices of the square are $\;(x_k,y_k) = \left\{(0,0),(1,0),(0,1),(1,1)\right\} , \; k=0,1,2,3\;$ . Each of the vertices can be, in principle With exception of $(x_0,y_0) = (0,0)$ ; this vertex is always inside the strip. (You're lucky, otherwise you had to distinguish $3^4 = 81$ cases to begin with.) Now there are $3^3 = 27$ sub cases, in principle. They can be conveniently enumerated in a base $3$ number system . For example $210$ means that vertex $(1,0)$ is below the strip, vertex $(0,1)$ is inside the strip and vertex $(1,1)$ is above the strip: the number is read from the right to the left, i.e. towards the most significant digit (as usual). Because of the restriction $0 \le \phi < \pi$ only the cases $\;000 \cdots 111\;$ have to be considered. The other cases are a mirror of these if $0 \le \phi < 2\pi$ is allowed eventually. With one noteworthy exception, though, namely $010 \not \equiv 212$ ($\color{red}{red}$) . So here comes: $$ \begin{matrix} 000 & 001 & 002 & \color{red}{010} & 011 & 012 & 020 & 021 & 022 & 100 & 101 & 102 & 110 & 111 \\ 222 & 221 & 220 & \color{red}{212} & 211 & 210 & 202 & 201 & 200 & 122 & 121 & 120 & 112 & \\ & & & & & NOP & & NOP & NOP & NOP & & & & \end{matrix} $$ A picture says more than a thousand words:

It is seen that there are at most 11 sub cases that must be taken into account.

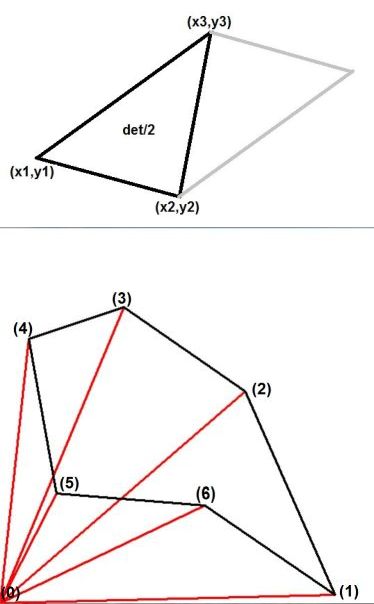
Area of polygon. Though at the moment we have only an impression of what the polygons look like, the areas of them have to be calculated, in the end.

So it's useful anyway to have a general method for doing just that. What we can do is to draw ($\color{red}{red}$) lines from the origin $(0)$ to the vertices of the polygon (six in our case) and sum up the areas of the (six) triangles $(0,1,2),(0,2,3),(0,3,4),(0,4,5),(0,5,6),(0,6,1)$ : see figure at the bottom. The figure at the top shows how the area of just one triangle is calculated, by using a determinant: $$ \mbox{area}\,\Delta = \frac{1}{2} det\begin{bmatrix}(x_2-x_1) & (y_2-y_1)\\(x_3-x_1) & (y_3-y_1)\end{bmatrix} $$ Note that, in general, the triangle areas thus calculated can be positive as well as negative. And the latter is essential.
To be continued for the coordinates of the polygons, in anti-clockwise order.

Clipping problem. Usually a polygon (strip) is clipped against the square. But in our case, the square is clipped against a strip. Once the ideas are clear, the algebra involved is very elementary. Hoping that the program below is more or less self-documentary: 

program Q901259;

type
  point = record
    x,y : double;
  end;
  polygon = array of point;

function Area(round : polygon) : double;
{
  Area of polygon
}
var
  k,L : integer;
  Det,Opp : double;
  p,q : point;
begin
  Opp := 0;
  L := Length(round);
  if L > 0 then
  begin
    q := round[L-1];
    for k := 0 to L-1 do
    begin
      p := q;
      q := round[k];
      Det := (p.x*q.y - q.x*p.y);
      Opp := Opp + Det;
    end;
  end;
  Area := Opp/2;
end;

function let(x,y : double) : point;
var
  P : point;
begin
  P.x := x; P.y := y;
  let := P;
end;

function x_is_0(c,p : double) : point;
begin
  x_is_0 := let(0,c/sin(p));
end;

function x_is_1(c,p : double) : point;
begin
  x_is_1 := let(1,(c-cos(p))/sin(p));
end;

function y_is_0(c,p : double) : point;
begin
  y_is_0 := let(c/cos(p),0);
end;

function y_is_1(c,p : double) : point;
begin
  y_is_1 := let((c-sin(p))/cos(p),1);
end;

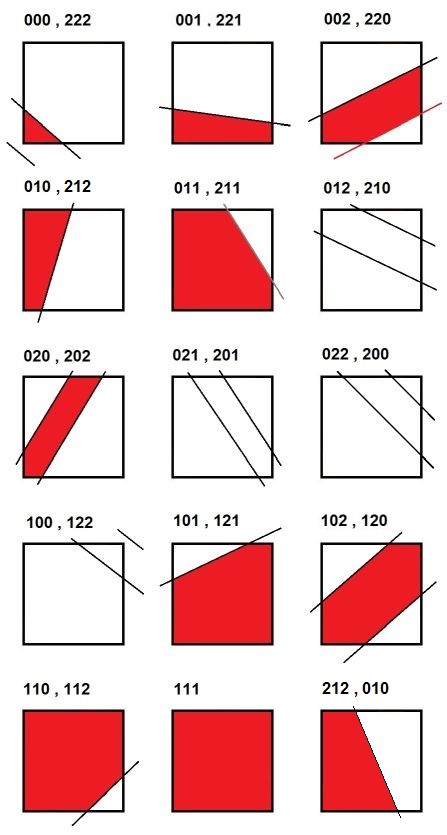
function Calculate(p,c : double) : double;
{
  Calculate area of strip inside square
   x*cos(p) + y*sin(p) = +/- c : strip
}
const
  choice : array[0..26] of integer =
  (0,1,2,3,4,-1,5,-1,-1,-1,6,7,8,9
  ,8,7,6,-1,-1,-1,5,-1,4,10,2,1,0);
var
  k,number,digit : integer;
  x,y : double;
  poly : polygon;
begin
  SetLength(poly,1);
  poly[0] := let(0,0);
  number := 0;

{Ternary number system }
  for k := 2 downto 0 do
  begin
    x := (k+1) mod 2;
    y := (k+1) div 2;
    digit := 1;
    if cos(p)*x+sin(p)*y < -c then digit := 0;
    if cos(p)*x+sin(p)*y > +c then digit := 2;
    number := number*3 + digit;
  end;

  {All sub cases }
  case choice[number] of
  0 :
    begin
      SetLength(poly,3);
      poly\[1] := y_is_0(+c,p);
      poly\[2] := x_is_0(+c,p);
    end;
  1 :
    begin
      SetLength(poly,4);
      poly\[1] := let(1,0);
      poly\[2] := x_is_1(+c,p);
      poly\[3] := x_is_0(+c,p);
    end;
  2 :
    begin
      SetLength(poly,5);
      poly\[1] := y_is_0(-c,p);
      poly\[2] := x_is_1(-c,p);
      poly\[3] := x_is_1(+c,p);
      poly\[4] := x_is_0(+c,p);
    end;
  3 :
    begin
      SetLength(poly,4);
      poly\[1] := y_is_0(-c,p);
      poly\[2] := y_is_1(-c,p);
      poly\[3] := let(0,1);
    end;
  4 :
    begin
      SetLength(poly,5);
      poly\[1] := let(1,0);
      poly\[2] := x_is_1(+c,p);
      poly\[3] := y_is_1(+c,p);
      poly\[4] := let(0,1);
    end;
  5 :
    begin
      SetLength(poly,5);
      poly\[1] := y_is_0(-c,p);
      poly\[2] := y_is_1(-c,p);
      poly\[3] := y_is_1(+c,p);
      poly\[4] := x_is_0(+c,p);
    end;
  6 :
    begin
      SetLength(poly,5);
      poly\[1] := let(1,0);
      poly\[2] := let(1,1);
      poly\[3] := y_is_1(+c,p);
      poly\[4] := x_is_0(+c,p);
    end;
  7 :
    begin
      SetLength(poly,6);
      poly\[1] := y_is_0(-c,p);
      poly\[2] := x_is_1(-c,p);
      poly\[3] := let(1,1);
      poly\[4] := y_is_1(+c,p);
      poly\[5] := x_is_0(+c,p);
    end;
  8 :
    begin
      SetLength(poly,5);
      poly\[1] := y_is_0(-c,p);
      poly\[2] := x_is_1(-c,p);
      poly\[3] := let(1,1);
      poly\[4] := let(0,1);
    end;
  9 :
    begin
      SetLength(poly,4);
      poly\[1] := let(1,0);
      poly\[2] := let(1,1);
      poly\[3] := let(0,1);
    end;
  10 :
    begin
      SetLength(poly,4);
      poly\[1] := y_is_0(+c,p);
      poly\[2] := y_is_1(+c,p);
      poly\[3] := let(0,1);
    end;
  end;
  Calculate := Area(poly);
end;

begin
  Random; Random;
{ Test }
  while true do
  begin
    Writeln(Calculate(Random*Pi,Random));
    Readln;
  end;
end.
But: is it possible to have a solution without all the sub case jazz? The answer is affirmative; that's how I actually tested the correctness of the above program. Any area can be simply determined by pixel counting (not necessarily in a "real" picture). Advantage: quick and dirty. Disadvantage: less exact than the sub case method.