Let $(x_1,y_1),(x_2,y_2),(x_3,y_3)$ be the vertices of the triangle. Then the three non-concurrent, non parallel lines can be represented by:
$$(y_2-y_1)(x-x_1)-(x_2-x_1)(y-y_1)=0$$
$$(y_3-y_2)(x-x_2)-(x_3-x_2)(y-y_2)=0$$
$$(y_1-y_3)(x-x_3)-(x_1-x_3)(y-y_3)=0$$
The coefficients in the OP's question are thus represented by:
$$
a_1 = (y_2-y_1) \quad ; \quad b_1 = -(x_2-x_1) \quad ; \quad c_1 = -(y_2-y_1)x_1+(x_2-x_1)y_1 \\
a_2 = (y_3-y_2) \quad ; \quad b_2 = -(x_3-x_2) \quad ; \quad c_2 = -(y_3-y_2)x_2+(x_3-x_2)y_2 \\
a_3 = (y_1-y_3) \quad ; \quad b_3 = -(x_1-x_3) \quad ; \quad c_3 = -(y_1-y_3)x_3+(x_1-x_3)y_3
$$
Now straightforward calculation should reveal that:
$$
\frac{det\begin{bmatrix}a_1 & b_1 & c_1\\a_2 & b_2 & c_2\\a_3 & b_3 & c_3\end{bmatrix}^2}{2C_1C_2C_3}
=\frac{1}{2} det\begin{bmatrix}(x_2-x_1) & (y_2-y_1)\\(x_3-x_1) & (y_3-y_1)\end{bmatrix}
$$
Where the latter (half) determinant certainly represents the area of the triangle:
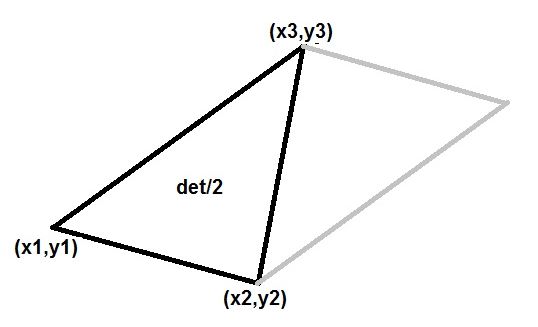
The algebra is somewhat tedious. Therefore I've invoked MAPLE to save time and effort:
A := array([[a1,b1,c1],[a2,b2,c2],[a3,b3,c3]]);
C1 := det(array([[a2,b2],[a3,b3]]));
C2 := -det(array([[a1,b1],[a3,b3]]));
C3 := det(array([[a1,b1],[a2,b2]]));
B := array([[x2-x1,y2-y1],[x3-x1,y3-y1]]);
verify(det(A)^2/(2*C1*C2*C3),det(B)/2,equal);
true
This completes the proof.
