Proof without words ( partial answer / informal proof ) .
Consider the following function:
$$
f(a,b) = \sqrt{(2a+1)^2+(2b-\dfrac{\sqrt{3}}{3})^2}
+ \sqrt{(2a-1)^2+(2b-\dfrac{\sqrt{3}}{3})^2}
+ \sqrt{4a^2+(2b+\dfrac{2\sqrt{3}}{3})^2} \\
- \sqrt{(a-1)^2+(b+\dfrac{\sqrt{3}}{3})^2}
- \sqrt{(a+1)^2+(b+\dfrac{\sqrt{3}}{3})^2}
- \sqrt{a^2+(b-\dfrac{2\sqrt{3}}{3})^2}
$$

Contour lines darker if closer to zero; coordinate axes in yellow.
- Picture on the left: contours of the function for $-3 < a < +3$ and $-3 < b < +3$ ;
contour levels $\in \left\{ 0.01,0.1,0.4,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 \right\}$ ;
the higher level lines appear to be circles.
- Picture on the right: contours of the function for $-0.1 < a < +0.1$ and $-0.1 < b < +0.1$ ;
contour levels $\in \left\{ 0.01,0.1,0.4,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 \right\} / 200$ ;
the low level lines appear to be circles as well (or ellipses ? ).
Brute force graphical/numerical evidence thus shows that the function is positive everywhere
and that the minimum is expected at $(a,b) = (0,0)$ ;
indeed $f(0,0) = 2\sqrt{1+1/3} + \sqrt{4/3} - 2\sqrt{1+1/3} - \sqrt{4/3} = 0$ .
Yes, I know this is not what people here finally want,
but I hope it helps to find a more satisfactory answer.
Geometrical meaning. As already present in the OP's question,
repeated here for convenience.
Let the origin be $O = (0,0)$ . $A = (-1,-\sqrt{3}/3)$ , $B = (+1,-\sqrt{3}/3)$ ,
$C = (0,+2\sqrt{3}/3)$ , which is an equilateral triangle with length of the edges $=2$ .
We choose a random point $\,\color{green}{Q = (a,b)}\,$
and define another point $\,\color{red}{P = (-2a,-2b)}$ .
The yellow lines are the coordinate system and $\overline{PQ}$ going through the origin $O$.
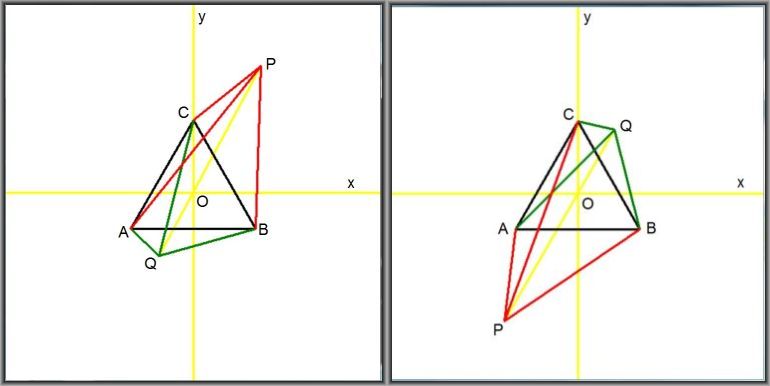
Then we have to prove that the sum of the red lengths is greater than the sum of the green lengths:
$\overline{PA} + \overline{PB} + \overline{PC} \ge \overline{QA} + \overline{QB} + \overline{QC}$ .
Which is beyond me at the moment being.


