Let's start with a few references to get an idea:
Interesting related issues:
Let the length of the blocks on the stack be two ($= 2$ in a certain physical unit) .
Assume that each block has a mass equal to one ($= 1$ in a certain physical unit) .
Then the center of gravity of a single block is given by: $Z_1 = 1$ .
Suppose the center of gravity of the first $(n)$ blocks is given by $Z_n$ ,
then add one block and find the new center of gravity $Z_{n+1}$ . Place
the new block with its left side underneath the old blocks, such that
they cannot collapse, i.e. left side exactly at $Z_n$ .
$Z_{n+1}$ is given by the mass of the previous $(n)$ blocks times the old center
of gravity, plus a distance equal to the old center of gravity (so that
the blocks will not collapse), plus one times one (= center of gravity
of the newly added block times its mass). The whole must be devided by
the new number of blocks. Hence the formula becomes:
$$
Z_{n+1} = (n.Z_n + Z_n + 1)/(n+1) \quad \Longrightarrow \quad Z_{n+1} = Z_n + \frac{1}{n+1}
$$
Starting with $n = 0$ and $Z_0 = 0$ this becomes:
$$
Z_1 = 1 \; , \; Z_2 = 1 + 1/2 \; , \; Z_3 = 1 + 1/2 + 1/3 \; , \;
Z_4 = 1 + 1/2 + 1/3 + 1/4 \; , \; \cdots
$$
which is precisely the Harmonic Series.
Where $Z_4 = 25/12$ and subsequent terms $> 2$ (= length of single block), yet the whole thing doesn't collapse.
But what we are really looking for is a continuous approximation of the
Harmonic Cantilever.
$$
\begin{array}{ll}
y = 0 & x = 0 \\
y = -1 & x = 1 \\
y = -2 & x = 1 + 1/2 \\
y = -3 & x = 1 + 1/2 + 1/3 \\
y = -4 & x = 1 + 1/2 + 1/3 + 1/5 \\
...........&................................ \\
y = -n & x = 1 + 1/2 + 1/3 + ... + 1/n \\
y = -(n+1) & x = 1 + 1/2 + 1/3 + ... + 1/n + 1/(n+1) \end{array}
$$
It is seen that $\;y(n+1) - y(n) = [ x(n+1) - x(n) ]\, y(n+1)$ .
For large $(n)$ , the finite differences $[ x(n+1) - x(n) ]$ become smaller
and smaller and the quotient $[ y(n+1) - y(n) ] / [ x(n+1) - x(n) ]$ is
an approximation of the differential quotient $dy/dx$ . Hence $dy/dx = y$ .
The solution of this differential equation is: $\;y = c \cdot \exp(x)$ . From the
above table, we read that $c < 0$ . A kind of best fit between the stack
of bricks in the Harmonic Cantilever and this function has been used to
determine the constant $(c)$ . A least squares minimalization procedure
has been used for this purpose:
$$
\sum_{k=1}^N \left[\; y_k - c e^{x_k}\; \right]^2 = \mbox{minimum}(c)
$$
Differentiating to $(c)$ and equating the result to zero then results in:
$$
c = \frac{\sum_{k=1}^N y_k.e^{x_k}}{\sum_{k=1}^N e^{2\,x_k}}
$$
Where $y_k = -1, -2, -3, .. , -N$ .
And $x_k = 1 \, ,\, 1 + 1/2 \, ,\, 1 + 1/2 + 1/3 \, ,\, \cdots \, ,\, 1 + 1/2 + 1/3 + .. + 1/N $
Here is the program that calculates the constant:
program LS;
function konstante : double;
{
Least Squared Best Fit
}
const
N : integer = 10000000;
var
y : integer;
x,u,v,p : double;
begin
x := 0;
u := 0; v := 0;
for y := 1 to N do
begin
p := exp(x);
x := x + 1/y;
u := u + y*p;
v := v + p*p;
end;
konstante := u/v;
end;
begin
Writeln('|c| =',konstante);
end.
Output (absolute value) :
|c| = 0.561459525677516
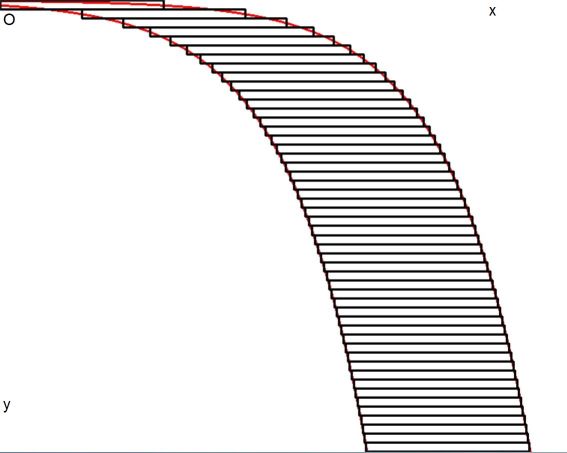
The result is shown in the following picture, for 50 bricks. Two best fit exponential
functions are displayed in $\color{red}{red}$ . The best fit exponential function on
the right can be formed from the best fit exponential function on the left by translating
the latter over a distance of two: $c\,\exp(x) \; \to \; c\,\exp(x-2)$ . So attention
may be restricted to the leftmost exponential.
So far so good: we have a numerical approximation for the best fit constant in the
exponential function (on the left). But the question is: can the constant $c$
in the conjectured best fit function be determined exactly ?
Write as follows:
$$
- y = - c\cdot e^x = e^{-G} e^x = e^{x-G}
$$
Take the logarithm at both sides and specify for values $\,y=-n$ :
$$
\ln(-y) = x-G \quad \Longleftrightarrow \quad \ln(n) = \sum_{k=1}^n \frac{1}{k} - G
$$
This especially remains valid for very large values of $\,n$ . In the limit:
$$
G = \lim_{n \to \infty} \left[ \sum_{k=1}^n \frac{1}{k} - \ln(n) \right] = \gamma
$$
Herewith it is proved that $\; |c| = e^{-\gamma}$ , where $\,\gamma\,$ is the
Euler–Mascheroni constant .
The complete solution is (see above picture) :
$$
\color{red}{left :} \quad y = - e^{x-\gamma} \qquad ; \qquad y = - e^{x-\gamma-2} \quad \color{red}{: right}
$$

