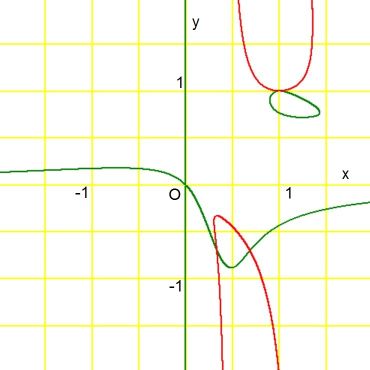

Note that $x$ is a factor of $g(x,y)$ , hence the $\color{green}{green}$ y-axis.
Also note that there are trivial solutions $(x,y,z) = \{(0,0,0),(1,1,1)\}\;$
and that the trivial solution $\,(x,y,z) = (0,0,0)\,$ is invisible.
The two non-trivial points where the two curves intersect are found numerically with MAPLE :
fsolve({f(x,y)=0,g(x,y)=0},{x,y},{x=0.5..1,y=-1..-0.5});
fsolve({f(x,y)=0,g(x,y)=0},{x,y},{x=0..0.5,y=-1..-0.5});
Our solution is (but not quite) in agreement with the answer found by
miracle173 :
$$
\left\{x = 0.6867320382, y = -0.7012678009, z = -1.430213436 \right\}\\
\left\{x = 0.3367211174, y = -0.7012678009, z = -0.343848349 \right\}
$$
But ah, what the OP probably wants is an analytical solution. So here comes / MAPLE says:
$$
\left\{ x={\frac {1}{72}}\,{\frac {9\, \left( 12+4\,\sqrt {5}
\right) ^{4/3}-48\,\sqrt {5}-48\,\sqrt [3]{12+4\,\sqrt {5}}+3\,\sqrt
{9\, \left( 12+4\,\sqrt {5} \right) ^{8/3}-96\, \left( 12+4\,\sqrt {5}
\right) ^{4/3}\sqrt {5}-96\, \left( 12+4\,\sqrt {5} \right) ^{5/3}-
3840+512\,\sqrt {5}\sqrt [3]{12+4\,\sqrt {5}}+1536\, \left( 12+4\,
\sqrt {5} \right) ^{2/3}-320\, \left( 12+4\,\sqrt {5} \right) ^{4/3}-
3072\,\sqrt {5}+768\, \left( 12+4\,\sqrt {5} \right) ^{2/3}\sqrt {5}}}
{ \left( 12+4\,\sqrt {5} \right) ^{2/3}}},y=-1/6\,\sqrt [3]{12+4\,
\sqrt {5}}-2/3\,{\frac {1}{\sqrt [3]{12+4\,\sqrt {5}}}} \right\}
$$ $$
\left\{ x={\frac {1}{72}}\,{\frac {9\, \left( 12+4\,\sqrt {5}
\right) ^{4/3}-48\,\sqrt {5}-48\,\sqrt [3]{12+4\,\sqrt {5}}-3\,\sqrt
{9\, \left( 12+4\,\sqrt {5} \right) ^{8/3}-96\, \left( 12+4\,\sqrt {5}
\right) ^{4/3}\sqrt {5}-96\, \left( 12+4\,\sqrt {5} \right) ^{5/3}-
3840+512\,\sqrt {5}\sqrt [3]{12+4\,\sqrt {5}}+1536\, \left( 12+4\,
\sqrt {5} \right) ^{2/3}-320\, \left( 12+4\,\sqrt {5} \right) ^{4/3}-
3072\,\sqrt {5}+768\, \left( 12+4\,\sqrt {5} \right) ^{2/3}\sqrt {5}}}
{ \left( 12+4\,\sqrt {5} \right) ^{2/3}}},y=-1/6\,\sqrt [3]{12+4\,
\sqrt {5}}-2/3\,{\frac {1}{\sqrt [3]{12+4\,\sqrt {5}}}} \right\}
$$
And $z$ can be calculated from $\;z = 3xy-x-y\;$ .
Whatever .. What we see is that the $y$-coordinates of the two solutions are indeed exactly the same
and I would like to hear a simple argument for this.