Let's consider the simplest non-trivial finite element shape in two dimensions:
the linear triangle. Function behaviour is approximated inside such a triangle
by a linear interpolation between the function values at the vertices,
also called: nodal points. Let $T$ be such a function, and $(x,y)$ coordinates,
then:
$$
T = A.x + B.y + C
$$
Where the constants A, B, C are to be determined.
Substitute $ x=x_k $ and $ y=y_k $ with $ k=1,2,3 $:
$$
\left[ \begin{array}{c} T_1 \\ T_2 \\ T_3 \end{array} \right] =
\left[ \begin{array}{ccc} 1 & x_1 & y_1 \\
1 & x_2 & y_2 \\
1 & x_3 & y_3 \end{array} \right]
\left[ \begin{array}{c} C \\ A \\ B \end{array} \right]
$$
The first of these equations can already be used to eliminate the
constant $C$, once and forever:
$$
T_1 = A.x_1 + B.y_1 + C
$$
Resulting in:
$$
T - T_1 = A.(x - x_1) + B.(y - y_1)
$$
Hence the constants $A$ and $B$ are determined by:
$$ \begin{array}{ll}
T_2 - T_1 = A.(x_2 - x_1) + B.(y_2 - y_1) \\
T_3 - T_1 = A.(x_3 - x_1) + B.(y_3 - y_1)
\end{array} $$
Two equations with two unknowns. The solution is found by straightforward
elimination, or by applying Cramer's rule:
$$ \begin{array}{ll}
A = [ (y_3 - y_1).(T_2 - T_1) - (y_2 - y_1).(T_3 - T_1) ] / \Delta \\
B = [ (x_2 - x_1).(T_3 - T_1) - (x_3 - x_1).(T_2 - T_1) ] / \Delta
\end{array} $$
There are several forms of the determinant $\Delta$, which should be memorized when
it is appropriate:
\begin{eqnarray*}
&& \Delta = (x_2 - x_1).(y_3 - y_1) - (x_3 - x_1).(y_2 - y_1) \\
&& \Delta = 2 \times \mbox{ area of triangle } \\
&& \Delta = x_1.y_2 + x_2.y_3 + x_3.y_1 - y_1.x_2 - y_2.x_3 - y_3.x_1 \\
&& \Delta = x_1.(y_2 - y_3) + x_2.(y_3 - y_1) + x_3.(y_1 - y_2) \\
&& \Delta = y_1.(x_3 - x_2) + y_2.(x_1 - x_3) + y_3.(x_2 - x_1) \\
&& \Delta = \left\| \begin{array}{ccc} 1 & x_1 & y_1 \\
1 & x_2 & y_2 \\
1 & x_3 & y_3 \end{array} \right\|
\end{eqnarray*}
Anyway, it is concluded that:
$$
T - T_1 = \xi.(T_2 - T_1) + \eta.(T_3 - T_1)
$$ Where:
$$ \begin{array}{ll}
\xi = [ (y_3 - y_1).(x - x_1) - (x_3 - x_1).(y - y_1) ] / \Delta \\
\eta = [ (x_2 - x_1).(y - y_1) - (y_2 - y_1).(x - x_1) ] / \Delta
\end{array} $$
Or:
$$
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right] =
\left[ \begin{array}{cc} + (y_3 - y_1) & - (x_3 - x_1) \\
- (y_2 - y_1) & + (x_2 - x_1)
\end{array} \right] / \Delta
\left[ \begin{array}{c} x - x_1 \\ y - y_1 \end{array} \right]
$$
The inverse of the following problem is recognized herein:
$$
\left[ \begin{array}{c} x - x_1 \\ y - y_1 \end{array} \right] =
\left[ \begin{array}{cc} (x_2 - x_1) & (x_3 - x_1) \\
(y_2 - y_1) & (y_3 - y_1)
\end{array} \right]
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right]
$$
Or:
$$ \begin{array}{ll}
x - x_1 = \xi .(x_2 - x_1) + \eta.(x_3 - x_1) \\
y - y_1 = \xi .(y_2 - y_1) + \eta.(y_3 - y_1)
\end{array} $$
But also:
$$
T - T_1 = \xi .(T_2 - T_1) + \eta.(T_3 - T_1)
$$
Therefore the same expression holds for the function $T$ as well as for
the coordinates $x$ and $y$ . This is precisely what people mean by an
isoparametric ("same parameters") transformation, a terminology which is
quite common in Finite Element contexts.
Now recall the formulas which express $\xi$ and $\eta$ into $x$ and $y$ :
$$ \begin{array}{ll}
\xi = [ (y_3 - y_1).(x - x_1) - (x_3 - x_1).(y - y_1) ]/\Delta \\
\eta = [ (x_2 - x_1).(y - y_1) - (y_2 - y_1).(x - x_1) ]/\Delta
\end{array} $$
Thus $\xi$ can be interpreted as: area of the sub-triangle spanned by the
vectors $ (x - x_1 , y - y_1) $ and $ (x_3 - x_1 , y_3 - y_1) $
divided by the whole triangle area.
And $\eta$ can be interpreted as: area of the sub-triangle spanned by the
vectors $ (x - x_1 , y - y_1) $ and $ (x_2 - x_1 , y_2 - y_1) $
divided by the whole triangle area.
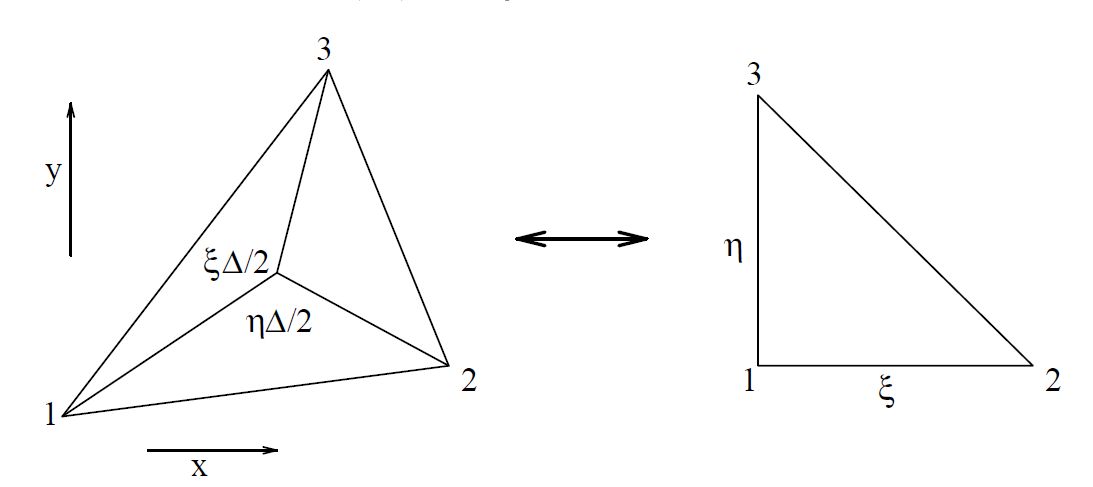
This is the reason why $ \xi $ and $ \eta $ are sometimes called
area-coordinates; see the figure below, where (two times) the area of the
triangle as a whole is denoted as $\Delta$.
There exist even three of these coordinates in literature. But
the third area-coordinate is, of course, dependent on the other two,
being equal to $(1-\xi-\eta)$.
Instead of area-coordinates, we prefer to talk about local coordinates
$\xi$ and $\eta$ of an element, in contrast to the global coordinates
$x$ and $y$.
It is possible that local coordinates coincide with the global coordinates.
A triangle for which such is the case is called a parent element.
The portrait of the parent triangle is also depicted in the same figure:
the two sides of it are coincident with the unit vectors in a Cartesian
coordinate system.
So far so good about standard FEM.
Now about your real problem (I hope).
Suppose you have two triangles, one with coordinates
$\left\{ (x_1,y_1), (x_2,y_2), (x_3,y_3) \right\} $ and one with coordinates
$\left\{ (x'_1,y'_1), (x'_2,y'_2), (x'_3,y'_3) \right\} $, then it is always
possible to transform the first triangle into the second via the parent element.
As follows.
$$
\left[ \begin{array}{c} x - x'_1 \\ y - y'_1 \end{array} \right] =
\left[ \begin{array}{cc} (x'_2 - x'_1) & (x'_3 - x'_1) \\
(y'_2 - y'_1) & (y'_3 - y'_1)
\end{array} \right]
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right]
$$
$$
\left[ \begin{array}{c} \xi \\ \eta \end{array} \right] =
\left[ \begin{array}{cc} (x_2 - x_1) & (x_3 - x_1) \\
(y_2 - y_1) & (y_3 - y_1)
\end{array} \right]^{-1}
\left[ \begin{array}{c} x - x_1 \\ y - y_1 \end{array} \right]
$$
The resulting transformation is independent of rotation and scaling of the
global coordinates, i.e. it leaves similarities intact at both sides.
So if you have two sample triangles that are transformed into each other,
then all triangles that are similar to those two are transformed in the same way.
