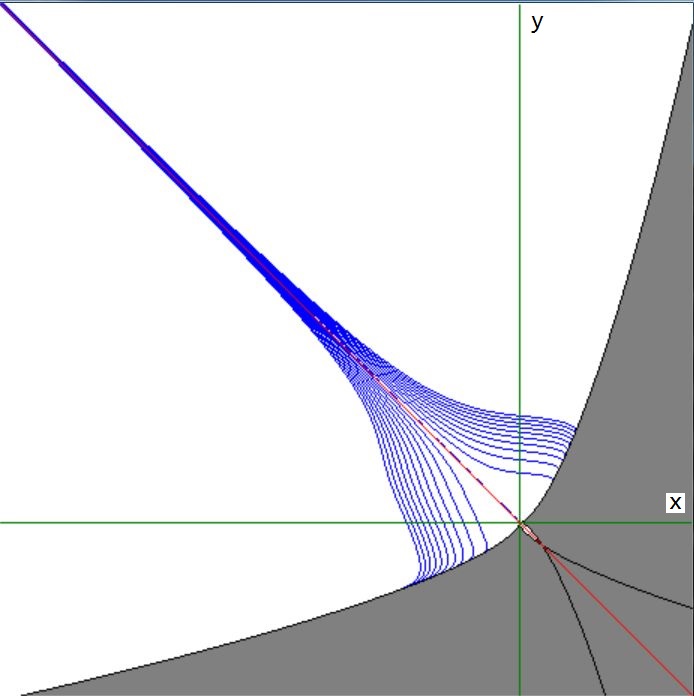
Below some characteristics of the function $f(x,y) = \left(\sqrt{y^2-x^3}-x\right)\left(\sqrt{x^2+y^3}-y\right)-y^3$ are shown.
The area where $f(x,y)$ is undefined is in gray: $y^2 - x^3 < 0$ or $x^2 + y^3 < 0 $. Therefore the domain of the function
is mainly restricted to $x\le 0$ and $y\ge 0$. The line $x+y=0$ is in red, some contour lines of $f(x,y)$ are in blue.
The function is somewhat symmetrical around $x+y=0$, but not quite. Shouldn't the restriction $x\le 0$ and $y\ge 0$ be added
to the problem in the first place?
It's easy to prove that $x+y=0$ is a solution of $f(x,y)=0$, but proving the reverse
seems to be tedious; at least I see no "nice" way to do it.