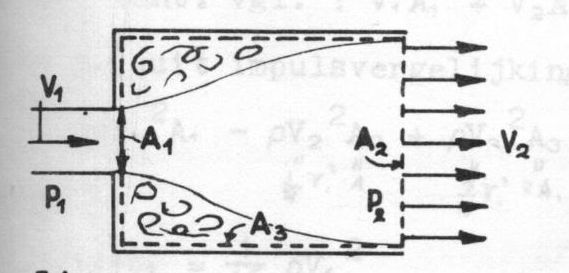

First define a closed control volume as indicated in the picture (dotted line).
Assumptions are: incompressible fluid, uniform velocity distribution over $A_1$ and $A_2$, friction along $A_3$ negligible.
Known quantities: pressure $p_1$, areas $A_1$, $A_2$, velocity $V_1$.
Then $V_2$ follows from integrating the continuity (partial differential) equation over the control volume, giving: $$V_2 A_2 = V_1 A_1$$
Next find $(p_2 - p_1)$ from integrating the momentum (partial differential) equation in $x$-direction,
if written as in the book: $$ \iint_A \rho u (\vec{v}\cdot\vec{n}) df = - \iint_A p \cos(n,x) df $$
Giving: $$ - \rho V_1^2 A_1 + \rho V_2^2 A_2 = p_1 A_2 - p_2 A_2 $$
Combining this with the continuity equation gives the unknown pressure $p_2$ as:
$$ p_2 = p_1 + \rho V_2 (V_1 - V_2) $$
There are plenty examples as well with the integral (instead of the differential) formulations of Electromagnetism.