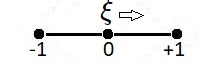
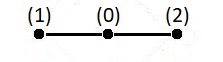


Algebraically, for any (Test) function $\,T(\xi)$ , it is defined by a quadratic interpolation, part of a Taylor series expansion: $$ T = T(0) + \frac{\partial T}{\partial \xi}(0).\xi + \frac{1}{2} \frac{\partial^2 T}{\partial \xi^2}(0).\xi^2 $$ Because of the mapping $(T_1,T_0,T_2) \to (-1,0,+1)$ it follows that: $$ T_0 = T(0)\\ T_1 = T(0) - \frac{\partial T}{\partial \xi}(0) + \frac{1}{2} \frac{\partial^2 T}{\partial \xi^2}(0)\\ T_2 = T(0) + \frac{\partial T}{\partial \xi}(0) + \frac{1}{2} \frac{\partial^2 T}{\partial \xi^2}(0)\\ \quad \mbox{ F.E. } \leftarrow \mbox{ F.D. } $$ Solving these equations is not much of a problem and well-known Finite Difference schemes are recognized: $$ T(0) = T_0 \\ \frac{\partial T}{\partial \xi}(0) = \frac{T_2-T_1}{2}\\ \frac{\partial^2 T}{\partial \xi^2}(0) = T_1-2T_0+T_2 \\ \quad \mbox{ F.D. } \leftarrow \mbox{ F.E. } $$ Finite Element shape functions may be constructed as follows: $$ T = N_0.T_0 + N_1.T_1 + N_2.T_2 = \\ T_0 + \frac{T_2-T_1}{2}\xi + \frac{T_1-2T_0+T_2}{2}\xi^2 =\\ (1-\xi^2)T_0 + \frac{1}{2}(-\xi+\xi^2)T_1 + \frac{1}{2}(+\xi+\xi^2)T_2 \\ \Longrightarrow \quad \begin{cases} N_0 = 1-\xi^2 \\ N_1 = (-\xi+\xi^2)/2\\ N_2 = (+\xi+\xi^2)/2 \end{cases} $$ Isoparametric means that the same interpolation will be employed for any other function at the element. The global one-dimensional Cartesian coordinate $\,x\,$ itself may serve as an outstanding example of such another function: $$ x = x(0) + \frac{\partial x}{\partial \xi}(0).\xi + \frac{1}{2} \frac{\partial^2 x}{\partial \xi^2}(0).\xi^2\\ x = x_0 + \frac{x_2-x_1}{2}.\xi + \frac{1}{2} (x_1-2x_0+x_2).\xi^2\\ x = (1-\xi^2)x_0 + (-\frac{1}{2}\xi+\frac{1}{2}\xi^2).x_1 + (+\frac{1}{2}\xi+\frac{1}{2}\xi^2).x_2 $$ Before trying to establish the inverse transformation - which means solving for $\,\xi$ - we make some substitutions. First assume that $\,x_1 < x_0 < x_2$ ; then define Left arm $\,L = x_0 - x_1\,$ and Right arm $\,R = x_2-x_0\,$ of the element:
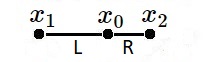
Algebraically:
$$
x = x_0 + \frac{x_2-x_1}{2}.\xi + \frac{1}{2} (x_1-2x_0+x_2).\xi^2 \\ \Longrightarrow \quad
\frac{R-L}{2}\xi^2 + \frac{R+L}{2}\xi + x_0 = x \\ \Longrightarrow \quad
x(\xi) = \frac{R-L}{2}\left[\xi + \frac{R+L}{2(R-L)}\right]^2 - \frac{R+L}{8(R-L)} + x_0
$$
This means that the curve $\,x(\xi)\,$ is a parabola for $\,R\ne L\,$ and linear for $\,R=L\,$ . Let's assume in the sequel
that our element is not the important special case, which is linear.
If $\,R\ne L$ , then the parabola $\,x(\xi)\,$ is convex and has a minimum for $\,R > L$ , is concave and and has a maximum for $\,R < L$ .
A few numerical experiments shall reveal what's going on.
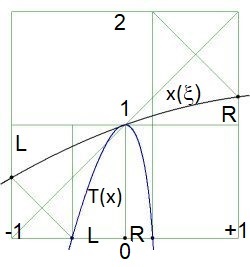
In the pictures below the viewport is $\,[-1,+1]\times[0,2]$ .
Curve in black is the function $\,x(\xi)\,$ with $\,x_0=1$ , curve in
$\color{blue}{blue}$ is an isoparametric Test function $\,T(\xi) = 1-\xi^2\,$ with $\,x_0=0$ . Thin lines in $\color{green}{green}$ are
for support of the ideas. Regular behavior without any anomalies is displayed first, for $\,R < L$ , $R \approx L$ , $R > L$ :
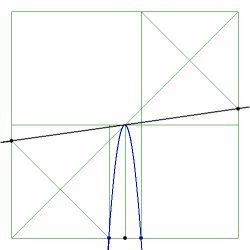
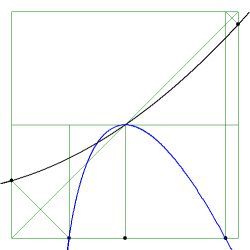
$\color{red}{Red}$ dots indicate anomalous behavior. Resulting in a Test function which is multi-valued outside the element, ipse est (i.e.):
not a function at all. It is seen in the pictures that such is the case if the maximum or minimum of the parabola $\,x(\xi)\,$
is inside the parent element $[-1,+1]$ domain:
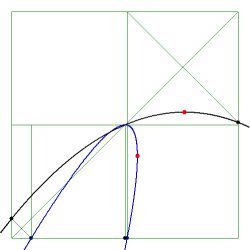
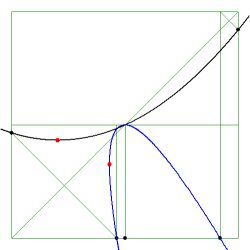
Therefore, to avoid anomalous behavior, the position of the extreme of the parabola must be outside the $[-1,+1]$
range of the parent element:
$$
-\frac{R+L}{2(R-L)} < -1 \quad \mbox{and} \quad -\frac{R+L}{2(R-L)} > +1
$$
Written otherwise:
$$
-\frac{R+L}{2(R-L)} + 1 < 0 \quad \Longleftrightarrow \quad
\frac{R-3L}{2(R-L)} < 0 \quad \Longleftrightarrow \quad \frac{R/L-3}{2(R/L-1)} < 0 \\
-\frac{R+L}{2(R-L)} - 1 > 0 \quad \Longleftrightarrow \quad
\frac{-3R+L}{2(R-L)} > 0 \quad \Longleftrightarrow \quad \frac{L/R-3}{2(L/R-1)} < 0
$$
Thus we only have to solve for the first inequality and then exchange $\,L \leftrightarrow R$ . Here goes:
$$
R/L - 1 < 0 \quad \Longrightarrow \quad R/L-3 > 0 \quad \Longrightarrow \quad
\begin{cases} R/L > 3 \\ R/L < 1 \end{cases} \quad \mbox{: impossible}
$$
But there is another possibility, though only one:
$$
R/L - 1 > 0 \quad \Longrightarrow \quad R/L-3 < 0 \quad \Longrightarrow \quad
\begin{cases} R/L < 3 \\ R/L > 1 \end{cases}
$$
At last, in view of the above, with $\,L \leftrightarrow R$ :
$$
\begin{cases} L/R < 3 \\ L/R > 1 \end{cases} \quad \mbox{and} \quad
\begin{cases} R/L < 3 \\ R/L > 1 \end{cases} \quad \Longrightarrow \quad
\begin{cases} 1/3 < R/L < 3 \\ R/L \ne 1 \end{cases}
$$
It is concluded that the one-dimensional quadratic finite element is useful if and only if the quotient of the two arms lengths
is between rather narrow boundaries. It must be not to far from linear, so to speak:
$$
\frac{\mbox{long arm}}{\mbox{short arm}} < 3
$$
Otherwise you run the risk of having spurious behaviour, which may be even worse - and more difficult to trace - in two or three
dimensions. That's one reason why I am definitely in favour of linear instead of higher order (say quadratic) elements.
Note. Anomalous behavior of the kind is also observed in 2-D, e.g. with quadrilateral elements having an obtuse angle or being self-intersecting. See : Quadrilateral Finite Elements must be convex and not self-intersecting. But why? .
Sad remark. A detailed analysis as the one above requires little more than some simple algebra and elementary geometry. Yet such an analysis is seldom seen in Finite Element contexts; though the conclusions of such an analysis seem to be important enough. So one can only guess for the reasons why it is not done.