 →
→  →
→ 
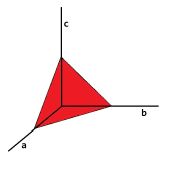
The three dimensional problem can be simplified to a two dimensional problem by introducing
(again
and again)
suitable triangle coordinates:
$$
\left[ \begin{array}{c} a \\ b \\ c \end{array} \right] =
\left[ \begin{array}{c} 3 \\ 0 \\ 0 \end{array} \right] +
\left[ \begin{array}{c} -3 \\ 3 \\ 0 \end{array} \right] x +
\left[ \begin{array}{c} -3 \\ 0 \\ 3 \end{array} \right] y
$$
Then the equation $(a^2+bc^4)(b^2+ca^4)(c^2+ab^4) \leq 64$ does not so much "simplify", but anyway becomes an equation in two
variables (2-D). And the equation $\;a + b + c = 3\;$ corresponds with a normed 2-D triangle, with vertices $(0,0),(1,0),(0,1)$ .
The insides of both can easily be visualized, as has been done in the above picture in the middle:
$\color{red}{red}$ for $\;a + b + c = 3\;$
and $\color{green}{green}$ for $\;(a^2+bc^4)(b^2+ca^4)(c^2+ab^4) \leq 64\;$ .
The transformed inequality is:
$$\left[ 3^2\left( 1-x-y \right)^{2} + 3^5\,x{y}^{4} \right]
\left[ 3^2\,{x}^{2} + 3^5\,y \left( 1-x-y \right)^{4} \right]
\left[ 3^2\,{y}^{2} + 3^5\, \left( 1-x-y \right){x}^{4} \right] \le 64
$$
It is seen in the same picture that the edge $\;y=1-x\;$ of the triangle maybe is tangent to the curve $(a^2+bc^4)(b^2+ca^4)(c^2+ab^4) = 64$ . Indeed, if we substitute $y=1-x$ into (the transformation of) that equation and simplify, then we get: $$ 3^9\, x^3 (1-x)^6 - 64 = 0 $$ The same sort of equation is found with the substitutions $\,x=0\,$ or $\,y=0\,$, for the other two edges. And, as has been found by others, there is only one solution of that equation, within the specified range, namely $x=1/3$, corresponding with $y=2/3$ and hence $(a,b,c) = (0,1,2)$ . And of course any cyclic permutation of this, due to symmetry. The rest of the (red) triangle $\;a + b + c = 3\;$ is well within the (green) area of $\;(a^2+bc^4)(b^2+ca^4)(c^2+ab^4) \leq 64$ . Which can be shown by plotting the triangle first: then it becomes absorbed by the green area (see picture on the right).
Analytically, the proof is completed by considering the function $\;f(x) = 3^9\, x^3 (1-x)^6$ .
Its extreme values are found for $\;f'(x) = x^2(1-x)^5(3-9x)=0$ , giving $\;x = \{0,1,1/3\}$ ,
with the maximum $\;f(1/3)=64$ .
The picture on the right shows the the inequality as observed in the plane $\;a + b + c = 3\;$ of the triangle in 3-D (picture on the left). Mind the symmetries.