The subject presented here is some content of the Wikipedia page about
Platonic solids
combined with my own experience on Finite Elements.
To start with the
latter, there is a standard piece of Finite Element theory concerning
triangles on MSE. The concept of isoparametrics is introduced herein. A reference to
the same theory is found in:
Is there any equation for triangle? (MSE).
So far so good for 2-D. In three dimensions the analogue of a triangle is
a tetrahedron. Let the parent tetrahedron have vertices (Finite Element
"nodes") that are numbered as follows:
$$
(0) = (0,0,0) \quad ; \quad (1) = (1,0,0) \quad ; \quad
(2) = (0,1,0) \quad ; \quad (3) = (0,0,1)
$$
Then any function with the parent tetrahedron can be interpolated as:
$$
f(\xi,\eta,\zeta) = (1-\xi-\eta-\zeta)f_0 + \xi\,f_1 + \eta\,f_2 + \zeta\,f_3
$$
Isoparametrics means that the same interpolation holds for the (global)
coordinates as well:
$$
x = (1-\xi-\eta-\zeta)x_0 + \xi \, x_1 + \eta \, x_2 + \zeta \, x_3 \\
y = (1-\xi-\eta-\zeta)y_0 + \xi \, y_1 + \eta \, y_2 + \zeta \, y_3 \\
z = (1-\xi-\eta-\zeta)z_0 + \xi \, z_1 + \eta \, z_2 + \zeta \, z_3
$$
From this the local parameters $(\xi,\eta,\zeta)$ can eventually be solved and
expressed in the global coordinates (which is not common practice, though).
Another frequently used Finite Element is the quadrilateral in 2-D or, quite analogously in 3-D: the hexahedron. The nodes of our parent element are: $$ (1) = (-1,-1,-1) \quad ; \quad (2) = (+1,-1,-1) \quad ; \quad (3) = (-1,+1,-1) \quad ; \quad (4) = (+1,+1,-1) \quad ; \quad (5) = (-1,-1,+1) \quad ; \quad (6) = (+1,-1,+1) \quad ; \quad (7) = (-1,+1,+1) \quad ; \quad (8) = (+1,+1,+1) $$ Then any function $h$ at the parent $h$exahedron can be interpolated as: $$ h(\xi,\eta,\zeta) = \frac{1}{8}(1-\xi)(1-\eta)(1-\zeta) h_1 + \frac{1}{8}(1+\xi)(1-\eta)(1-\zeta) h_2 + \frac{1}{8}(1-\xi)(1+\eta)(1-\zeta) h_3 + \frac{1}{8}(1+\xi)(1+\eta)(1-\zeta) h_4 + \frac{1}{8}(1-\xi)(1-\eta)(1+\zeta) h_5 + \frac{1}{8}(1+\xi)(1-\eta)(1+\zeta) h_6 + \frac{1}{8}(1-\xi)(1+\eta)(1+\zeta) h_7 + \frac{1}{8}(1+\xi)(1+\eta)(1+\zeta) h_8 $$ Note that this interpolation, in general, is not linear. And it's not so easy anymore to solve for the global coordinates ( by substituting $h = x,y,z$ ).
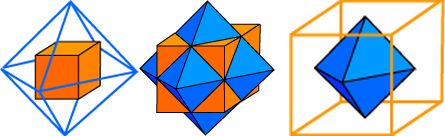
The following is a possible generalization of a finite element which was questioned about in: Understand 1D FEM solution using quadratics elements (MSE). In three dimensions we have the quite common Finite Difference Star, which is a not so common Finite Element, namely an octahedron augmented with the origin as an additional node $(0)$: $$ (0) = (0,0,0) \quad ; \quad (1) = (-1,0,0) \quad ; \quad (2) = (+1,0,0) \quad ; \quad (3) = (0,-1,0) \quad ; \quad (4) = (0,+1,0) \quad ; \quad (5) = (0,0,-1) \quad ; \quad (6) = (0,0,+1) $$ Then any function $s$ with the parent octahedron (F.D. $s$tar) can be interpolated as: $$ s(\xi,\eta,\zeta) = (1 - \xi^2 - \eta^2 - \zeta^2) s_0 + \frac{1}{2}\xi (\xi-1) s_1 + \frac{1}{2}\xi (\xi+1) s_2 + \frac{1}{2}\eta (\eta-1) s_3 + \frac{1}{2}\eta (\eta+1) s_4 + \frac{1}{2}\zeta (\zeta-1) s_5 + \frac{1}{2}\zeta (\zeta+1) s_6 $$ But now Wikipedia is consulted and the following is read in the chapter Dual polyhedra:
The other way around, we construct the dual of an arbitrary hexahedron, which is (not quite) an arbitrary octahedron: $$ s_1 = (h_1 + h_3 + h_5 + h_7)/4 \quad ; \quad s_2 = (h_2 + h_4 + h_6 + h_8)/4 \\ s_3 = (h_1 + h_2 + h_5 + h_6)/4 \quad ; \quad s_4 = (h_3 + h_4 + h_7 + h_8)/4 \\ s_5 = (h_1 + h_2 + h_3 + h_4)/4 \quad ; \quad s_6 = (h_5 + h_6 + h_7 + h_8)/4 \\ s_0 = (s_1 + s_2 + s_3 + s_4 + s_5 + s_6)/6 $$ Substitute this into the abovementioned expression for $s(\xi,\eta,\zeta)$ and simplify. The outcome (with a little help from Maple) is, again to my surprise: $$ \frac{1}{8}\left[ \,( h_1+h_2+h_3+h_4+h_5+h_6+h_7+h_8) \\ + (-h_1+h_2-h_3+h_4-h_5+h_6-h_7+h_8)\xi \\ + (-h_1-h_2+h_3+h_4-h_5-h_6+h_7+h_8)\eta \\ + (-h_1-h_2-h_3-h_4+h_5+h_6+h_7+h_8)\zeta \,\right] $$ The interpolation with the dual octahedron of an arbitrary hexahedron is linear again.
At last, according to
Wikipedia:
In all dimensions higher than four, there are only three convex regular
polytopes: the simplex, the hypercube, and the cross-polytope. In three
dimensions, these coincide with the tetrahedron, the cube, and the octahedron.
Where the (self-dual, linear) simplex may be considered as a trivial case.
Question. In all dimensions higher than three, does the isoparametric transformation give a linear interpolation for an arbitrary function discretized at the dual polytope of a "finite element" with the hypercube or the cross-polytope as a parent?
First case: the HyperCube as the dual polytope of the PolyStar. The following steps have been taken in order to obtain an answer.
S0 := 1-c1^2-c2^2-c3^2; S1 := c1*(c1-1)/2; S2 := c1*(c1+1)/2; S3 := c2*(c2-1)/2; S4 := c2*(c2+1)/2; S5 := c3*(c3-1)/2; S6 := c3*(c3+1)/2;
g := g0*S0+g1*S1+g2*S2+g3*S3+g4*S4+g5*S5+g6*S6;
f1 := eval(g,{c1=-1,c2=-1,c3=-1});
f2 := eval(g,{c1=+1,c2=-1,c3=-1});
f3 := eval(g,{c1=-1,c2=+1,c3=-1});
f4 := eval(g,{c1=+1,c2=+1,c3=-1});
f5 := eval(g,{c1=-1,c2=-1,c3=+1});
f6 := eval(g,{c1=+1,c2=-1,c3=+1});
f7 := eval(g,{c1=-1,c2=+1,c3=+1});
f8 := eval(g,{c1=+1,c2=+1,c3=+1});
H1 := (1-c1)/2*(1-c2)/2*(1-c3)/2; H2 := (1+c1)/2*(1-c2)/2*(1-c3)/2; H3 := (1-c1)/2*(1+c2)/2*(1-c3)/2; H4 := (1+c1)/2*(1+c2)/2*(1-c3)/2; H5 := (1-c1)/2*(1-c2)/2*(1+c3)/2; H6 := (1+c1)/2*(1-c2)/2*(1+c3)/2; H7 := (1-c1)/2*(1+c2)/2*(1+c3)/2; H8 := (1+c1)/2*(1+c2)/2*(1+c3)/2; f := f1*H1+f2*H2+f3*H3+f4*H4+f5*H5+f6*H6+f7*H7+f8*H8;
sort(simplify(f));Resulting in:$$ -1/2\,{\it c1}\,{\it g1}+1/2\,{\it c1}\,{\it g2}-1/2\,{\it c2}\,{\it g3}+1/2\,{\it c2}\,{\it g4}-1/2\,{\it c3}\,{\it g5}+1/2\,{\it c3}\,{ \it g6}-2\,{\it g0}+1/2\,{\it g1}+1/2\,{\it g2}+1/2\,{\it g3}+1/2\,{ \it g4}+1/2\,{\it g5}+1/2\,{\it g6}$$ By visual inspection, we see that the result is indeed linear in the $c_k$ coordinates.
Second case: the PolyStar as the dual polytope of the HyperCube. The following steps have been taken in order to obtain an answer.
g0 := eval(f,{c1=0,c2=0,c3=0});
g1 := eval(f,{c1=-1,c2=0,c3=0});
g2 := eval(f,{c1=+1,c2=0,c3=0});
g3 := eval(f,{c1=0,c2=-1,c3=0});
g4 := eval(f,{c1=0,c2=+1,c3=0});
g5 := eval(f,{c1=0,c2=0,c3=-1});
g6 := eval(f,{c1=0,c2=0,c3=+1});
sort(simplify(g));Resulting in:$$ -1/8\,{\it c1}\,{\it f1}+1/8\,{\it c1}\,{\it f2}-1/8\,{\it c1}\,{\it f3}+1/8\,{\it c1}\,{\it f4}-1/8\,{\it c1}\,{\it f5}+1/8\,{\it c1}\,{ \it f6}-1/8\,{\it c1}\,{\it f7}+1/8\,{\it c1}\,{\it f8}-1/8\,{\it c2} \,{\it f1}-1/8\,{\it c2}\,{\it f2}+1/8\,{\it c2}\,{\it f3}+1/8\,{\it c2}\,{\it f4}-1/8\,{\it c2}\,{\it f5}-1/8\,{\it c2}\,{\it f6}+1/8\,{ \it c2}\,{\it f7}+1/8\,{\it c2}\,{\it f8}-1/8\,{\it c3}\,{\it f1}-1/8 \,{\it c3}\,{\it f2}-1/8\,{\it c3}\,{\it f3}-1/8\,{\it c3}\,{\it f4}+1 /8\,{\it c3}\,{\it f5}+1/8\,{\it c3}\,{\it f6}+1/8\,{\it c3}\,{\it f7} +1/8\,{\it c3}\,{\it f8}+1/8\,{\it f1}+1/8\,{\it f2}+1/8\,{\it f3}+1/8 \,{\it f4}+1/8\,{\it f5}+1/8\,{\it f6}+1/8\,{\it f7}+1/8\,{\it f8} $$ By visual inspection, we see that the result is again linear in the $c_k$ coordinates.
In this way, I've proved the Dual = Linear conjecture for spaces with dimension $N = 2,3,4,5,6,7,8$.
Then Maple gives up. And me too, for the moment being.
Here is the program that generates the input for Maple:
program maple;
type punt = array of integer;
function Letterlijk(nr : integer) : string; { Convert Natural to String } const cijfer : string = '0123456789'; var no,t,tel,wel : integer; vgl : string; c : char; begin no := nr; tel := 0; { Analysis } vgl := ''; while no > 0 do begin c := cijfer[(no mod 10) + 1]; vgl := vgl + c; no := no div 10; tel := tel + 1; end; wel := tel div 2; for t := 0 to wel-1 do begin c := vgl[t+1]; vgl[t+1] := vgl[tel-t]; vgl[tel-t] := c; end; if vgl = '' then vgl := '0'; Letterlijk := vgl; end;
function twee(power : integer) : integer; { Compute 2^power } var k : integer; h : integer; begin h := 1; for k := 1 to power do h := h shl 1; twee := h; end;
function crd_H(nr,N : integer) : punt; { Node Number -> Hypercube Vertex Coordinates } var P : punt; h,k : integer; begin h := nr-1; SetLength(P,N); for k := 1 to N do begin P[k-1] := 2*(h and 1)-1; h := h shr 1; end; crd_H := P; end;
function crd_S(nr,N : integer) : punt; { Node Number -> PolyStar Vertex Coordinates } var P : punt; b,v,k : integer; begin SetLength(P,N); for k := 1 to N do begin P[k-1] := 0; end; if nr > 0 then begin b := (nr-1) div 2; v := (nr-1) mod 2; P[b] := 2*v-1; end; crd_S := P; end;
procedure shapes_H(N : integer); { HyperCube Shape Functions } var k,h,i,D : integer; c,s : string; begin D := twee(N); for i := 1 to D do begin h := i-1; s := ' := '; for k := 0 to N-1 do begin c := Letterlijk(k+1); if (h and 1) = 0 then s := s + '(1-c' + c + ')/2*' else s := s + '(1+c' + c + ')/2*'; h := h shr 1; end; Writeln('H',i,Copy(s,1,Length(s)-1),';'); end; s := ''; for k := 1 to D do begin c := Letterlijk(k); s := s + 'f' + c + '*H' + c + '+'; end; Writeln('f := ',Copy(s,1,Length(s)-1),';'); end;
procedure shapes_S(N : integer); { PolyStar Shape Functions } var k,i : integer; c,s : string; begin s := ' := 1'; for k := 1 to N do begin c := Letterlijk(k); s := s + '-c' + c + '^2'; end; s := s + ';'; Writeln('S0',s); for i := 1 to 2*N do begin s := ' := '; c := Letterlijk((i+1) div 2); if (i mod 2) = 1 then s := s + 'c' + c + '*(c' + c + '-1)/2;' else s := s + 'c' + c + '*(c' + c + '+1)/2;'; Writeln('S',i,s); end; s := 'g := '; for k := 0 to 2*N do begin c := Letterlijk(k); s := s + 'g' + c + '*S' + c + '+'; end; Writeln(Copy(s,1,Length(s)-1),';'); end;
procedure test_H(N : integer); { Dual = Linear test for HyperCube in PolyStar } var k,D,i : integer; s,c : string; P : punt; begin shapes_S(N);
SetLength(P,N); D := twee(N); for k := 1 to D do begin c := Letterlijk(k); s := 'f' + c + ' := eval(g,{'; P := crd_H(k,N); for i := 1 to N do begin if P[i-1] = -1 then c := '-1'; if P[i-1] = +1 then c := '+1'; s := s + 'c' + Letterlijk(i) + '=' + c + ','; end; c := Letterlijk(N); Writeln(Copy(s,1,Length(s)-1),'});'); end;
shapes_H(N); Writeln('sort(simplify(f));'); end;
procedure test_S( N : integer); { Dual = Linear test for PolyStar in HyperCube } var k,i : integer; s,c : string; P : punt; begin shapes_H(N);
s := 'g0 := eval(f,{'; for i := 1 to N do s := s + 'c' + Letterlijk(i) + '=0,'; Writeln(Copy(s,1,Length(s)-1),'});'); SetLength(P,0); for k := 1 to 2*N do begin c := Letterlijk(k); s := 'g' + c + ' := eval(f,{'; P := crd_S(k,N); for i := 1 to N do begin if P[i-1] = 0 then c := '0'; if P[i-1] = -1 then c := '-1'; if P[i-1] = +1 then c := '+1'; s := s + 'c' + Letterlijk(i) + '=' + c + ','; end; c := Letterlijk(N); Writeln(Copy(s,1,Length(s)-1),'});'); end;
shapes_S(N); Writeln('sort(simplify(g));'); end;
begin { test_H(8); } { test_S(9); } test_H(3); Writeln; test_S(3); end.