Perfect 2-D Hashing
Author: Han de Bruijn
Date: 2006 November
This is actually a re-write of an article posted in 'sci.math' as the
(would be) thread 'Inverse Perfect Hashing'
Imagine a rectangular region which is placed quite arbitrarily inside
a rectangular grid. It is questioned which gridpoints are inside this
rectangular region.
A picture says more
than a thousand words: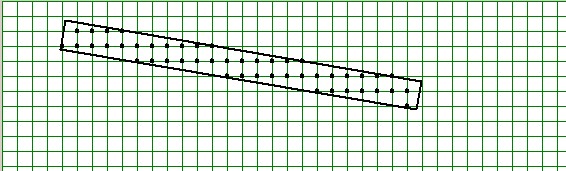
Forward Hash
Formulation of the problem
How to obtain a list of all grid points which are inside the rectangle,
where each grid point occurs only once in the list. And yes, we
want our algorithm to be as fast as possible.
Solution of the problem
The rectangle is transformed into a rectangle which coincides with a
cartesian coordinate system at two of its edges (i.e. the top-left position
becomes the origin in graphics coordinates). This is a translation combined
with a rotation. Each grid point is transformed into the translated/rotated
coordinates, giving (x,y) floating point values, instead of integer values:

When rounding the floating point values of the transformed interior points
to integer values, memory locations may be obtained, in principle.
Such a method is commonly called
hashing.
It can be demonstrated (: make a drawing) that at most two collisions can
happen when rounding these (x,y) coordinates: just try to bring two grid
points together in one grid cell. You will see that they can only fit in
if their mutual distance is smaller than √2, the diagonal of the cell:
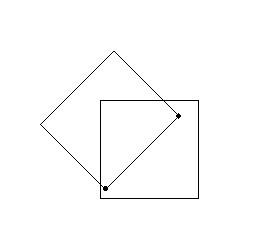
But two different grid points can oly give rise to the same round off values -
giving the midpoint of the grid cell - if they fit into the same grid cell.
The big trick is now that all lengths may be multiplied with this factor
√2 (preferrably even somewhat larger for safety):
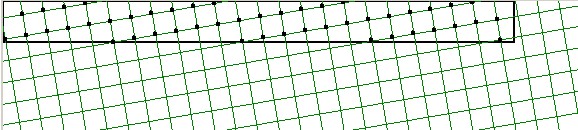
It is clear that all collisions have disappeared then: it's impossible to
bring two grid points with mutual distance greater than √2 together
into one 1x1 grid cell and round them to the same midpoint. With other words:
we have a perfect hash (though maybe it doesn't look like it, not yet):

But if these values are rounded . . . Look ! Here we are:

Therefore what we need is a table which is √2 times √2 =
twice as big as the minimal size which would be needed for storing all grid
point values "without gaps". The advantage of the overhead by a factor 2 is
that an adress is attached to a grid point immediately, without any need for
re-hashing (due to a collision) or searching.
Inverse Hash
Such a "Perfect Hash" can always be inverted. This is evident, because if
there is a one-to-one mapping of a grid point onto an adress then such a
mapping can always be inverted to a mapping of an adress onto a grid point.
The procedure is as follows. Traverse all adresses in our twice-too-big
table; and apply the inverse of all transformations in reverse order.
Inverse rounding in the first place, corresponding to plus or minus 1/2
with both coordinates, resulting in a little square with four vertices.
Then dividing all coordinates by √2 instead of a multiply. Rotate
over minus the angle, perform a translation backwards. The end-result of
this (floating point) procedure is the little square with, yes or no, a
grid point in it. Iff the grid point is within that little square, then
it can be found by rounding the coordinates of the center of the square.
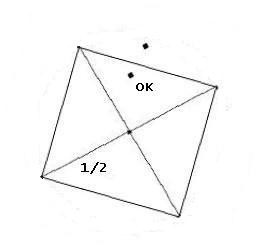
This center corresponds with the end-result by rounding, in the Forward
Hash procedure. Rounding the center gives whole-number coordinates, hence
a possible grid point. Next check if the candidate grid point is within
that little square as well. (This is not necessarily true: approximately
half of the grid points will be outside and approximately half of the grid
points will be inside the little square.) At last check if the
candidate grid point is within the large skew rectangle we started with.
In this manner, the Inverse Hashing procedure enables us to find all grid
points corresponding to adresses which can be filled with Forward Hashing.
Download
The above has been coded into a computer program. The main program produces
the pictures as captured and displayed in this web page. It is accompanied,
though, with a separate module (Delphi 'unit') called 'wiskunde' (Dutch for
'mathematics') and the above theory is embodied in this module. The source
code, together with a (Microsoft Windows) executable, is packed into a
downloadable ZIP file. Unpack in a spearate map
and eventually execute.
CG application
But look what we have obtained now ! Because grid points can be interpreted
as pixels - with Computer Graphics applications - Inverse Hashing is actually
a recursion-free Flood Fill procedure of arbitrary rectangles in an image.
The overhead measured in computation time is at most twice the theoretical
minimum, that is: iff each pixel could be found immediately, which in general
is not the case.
Number Theory
Key reference is the following article in the 'sci.math' thread ' 3^m/2^n => r '. The IMHO correct
statement is that any area equal to = 1 , in the 2-D grid of numerators and
denominators of fractions, contains at least zero and at most four fractions.
This means that, for a given r and ε , there must be a search up to
numerators or denominators with order of magnitude ( r / ε ) , if r
is the (irrational) number to be approximated and ε is the error
(tolerance) in the approximation.
Generalization
In three dimensional space, Perfect Hashing is accomplished by 3-D rotation,
translation and enlarging the rectangular box with a factor √3 in each
direction.
Disclaimers
Anything free comes without referee :-(
My English may be better than your Dutch.







