Product Function

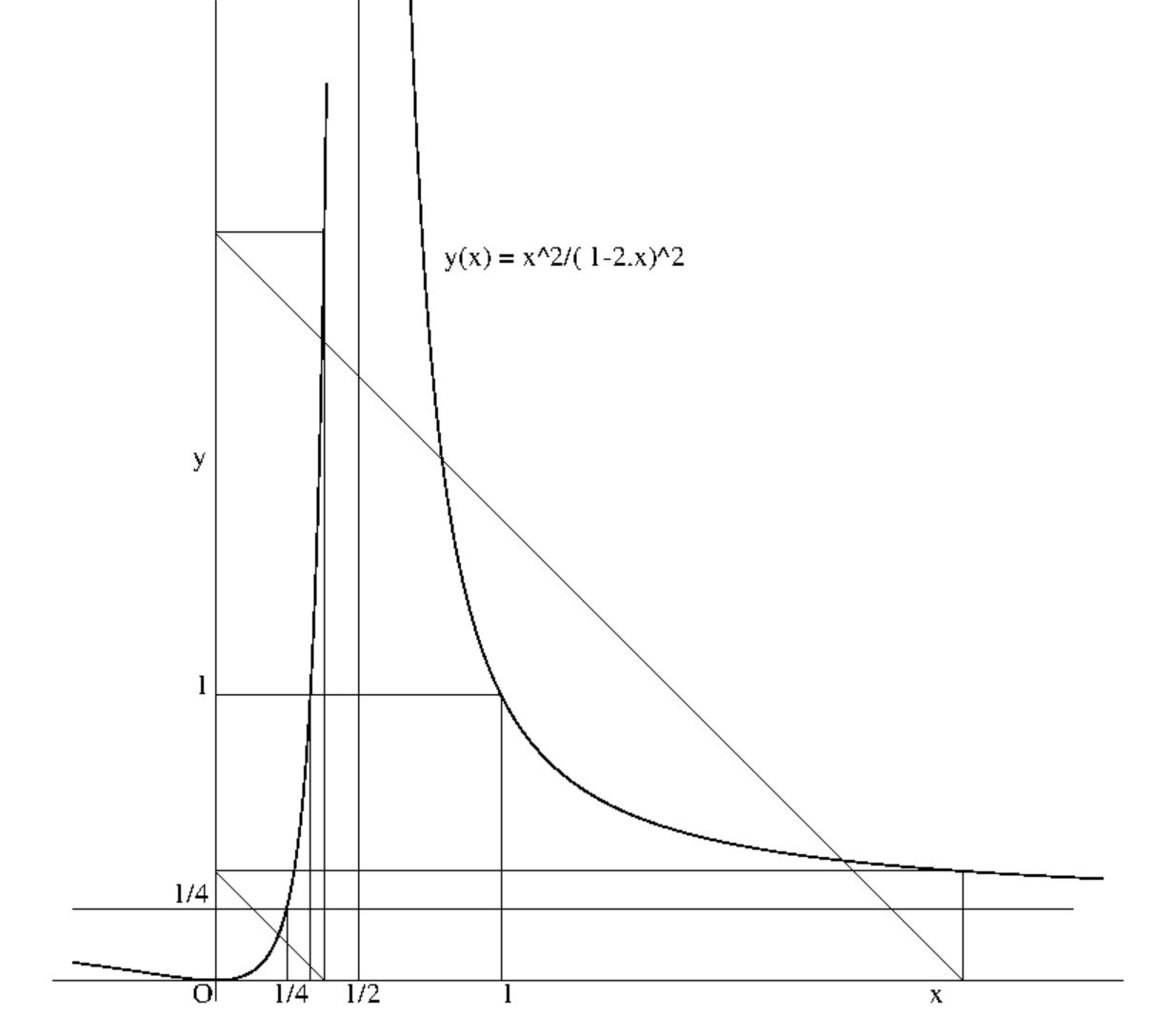
With grid coarsening, the function is used iteratively. Get started with a certain value of $x$ and the accompanying value of $y$ can be calculated. But this value of $y$ serves as the next $x$ value for the function $y$, as soon as the grid is coarsened again. In general, we obtain an assembly of the form: $$ y\left(y\left(y\left(y\left(y ... y(x)\right)\right)\right)\right) $$ It may be questioned if there exist values of $x$ which are are such that, after coarsening of the grid, the same value $x = y(x)$ is acquired again. Such values will remain the same during all stages of the grid coarsening process. For this reason, such values of $x$ are called stationary or invariant points of the function. They are found as follows: $$ x = \left( \frac{x}{2.x-1} \right)^2 \hieruit x = 0 \OF 1.(2.x-1)^2 = x \hieruit $$ $$ x^2 - \frac{5}{4} x + 1 = (x - 1)(x - \frac{1}{4}) = 0 $$ Herewith invariant points are found to be: $$ x = 0 \OF x = 1 \OF x = \kwart $$ The value $1/3$, being useful because of the condition $a.b < 1/3 < 1/2$, is mapped on the stationary value $1$: $$ \left( \frac{1/3}{1-2.1/3} \right)^2 = 1 $$ But the above list of invariant points is not exhaustive, another possibility being that there exist two points instead of one. After having obtained the point with label (1) in one iteration, the point with label (2) is reached in the next iteration. Then the point with label (1) is obtained again, and so on and so forth. We must solve an equation with $1/x$ instead of $x$: $$ \frac{1}{x} = \left( \frac{x}{2.x-1} \right)^2 \hieruit (2.x-1)^2 = x^3 \hieruit x^3 - 4.x^2 + 4.x - 1 = 0 $$ An equation of the third degree. However, we already know that $x=1/x=1$ must be a solution of it. Hence we can perform a division: $$ \frac{ x^3 - 4.x^2 + 4.x - 1 }{ x - 1 } = x^2 - 3.x + 1 = 0 $$ The roots of the equation are herewith found to be: $$ x_1 = 1 \OF x_2 = \frac{3}{2} + \frac{\sqrt{5}}{2} \approx 2.618 \OF x_3 = \frac{3}{2} - \frac{\sqrt{5}}{2} \approx 0.382 $$ Indeed: $x_1 = 1/x_1$ , $x_2 = 1/x_3$ and $x_3 = 1/x_2$. See the above figure.
Another interesting property of the invariant point $(1/4,1/4)$ can be found as follows. Consider the the expression $(1 - 4.a.b)$. We will derive a persistent property for it, by considering the expression while refining the mesh. We have found, in the previous chapter, that the product of the off-diagonal matrix coefficients is transformed as follows: $$ a.b = \frac{\sqrt{a'.b'}}{1 + 2.\sqrt{a'.b'}} $$ Herewith we find that $1 - 4.a.b$ is also transformed, according to: $$ 1 - 4.a.b = \frac{1 + 2.\sqrt{a'.b'} - 4.\sqrt{a'.b'}}{1 + 2.\sqrt{a'.b'}} = \frac{\left( 1 - 2.\sqrt{a'.b'} \right) \left( 1 + 2.\sqrt{a'.b'} \right) } {\left( 1 + 2.\sqrt{a'.b'} \right)^2 } = $$ $$ \frac{ 1 - 4.a'.b' } {\left( 1 + 2.\sqrt{a'.b'} \right)^2 } $$ Meaning that the sign of the $1 - 4.a.b$ is insensitive/invariant for for mesh refinement, persistent through multigrids: \begin{eqnarray*} 1 - 4.a.b \ge 0 \slechts 1 - 4.a'.b' \ge 0 \\ 1 - 4.a.b \le 0 \slechts 1 - 4.a'.b' \le 0 \end{eqnarray*} Thus if the expression is positive, then it remains positive. And if it is negative, then it remains negative. Last but not least, if it is zero, then it remains zero, the latter corresponding with the invariance of $(1/4,1/4)$. This may be translated as follows: $$ a.b \le \kwart \slechts a'.b' \le \kwart \qquad \EN \qquad a.b \ge \kwart \slechts a'.b' \ge \kwart $$ Hence the point $(1/4,1/4)$ serves as a boundary between two domains: points in the domain $x > 1/4$ will always give rise to other points $x$ with $x > 1/4$, while points in the domain $x < 1/4$ will always give rise to other points $x$ with $x < 1/4$. That's why discriminant is probably a good name for the expression $(1-4.a.b)$. With the sign of the discriminant, one can discriminate between two seemingly distinct domains of interest in $(a.b)$-space.
The properties $x'< x$ or $x'> x$ are persistent at MultiGrids. Let's prove it: $$ x' = x^2/(1 - 2.x)^2 < x \slechts 1 - 4.x + 4.x^2 > x \slechts x^2 - 5/4.x + 1/4 > 0 $$ The accompanying function is a parabola: $$ y = \left(x - \frac{5}{8}\right)^2 - \frac{25}{64} + \frac{16}{64} $$ Which has a minimum for $(x,y) = (5/8,-9/64)$. It is positive for: $$ (x - 1) (x - \kwart) > 0 $$ Ignoring the conditions $x>1$ and $x<1$, while $x<1/3<1/2$, results in: $$ x > x' \slechts x < \kwart \qquad ; \qquad x < x' \slechts x > \kwart $$ This means that products smaller than $1/4$ will become bigger and products bigger than $1/4$ will become smaller with grid refinement; any product of coefficients will approximate $1/4$ closer with successive refinement at uniform MultiGrids. We have seen that the latter outcome is persistent through further grid refinement. With other words, the point $1/4$ is a stationary point (attractor) of the Product Function for grid refinement. It can also be said that $1/4$ repels the products during the reverse process, of grid coarsening. Click On Pic for viewing the PostScript code:

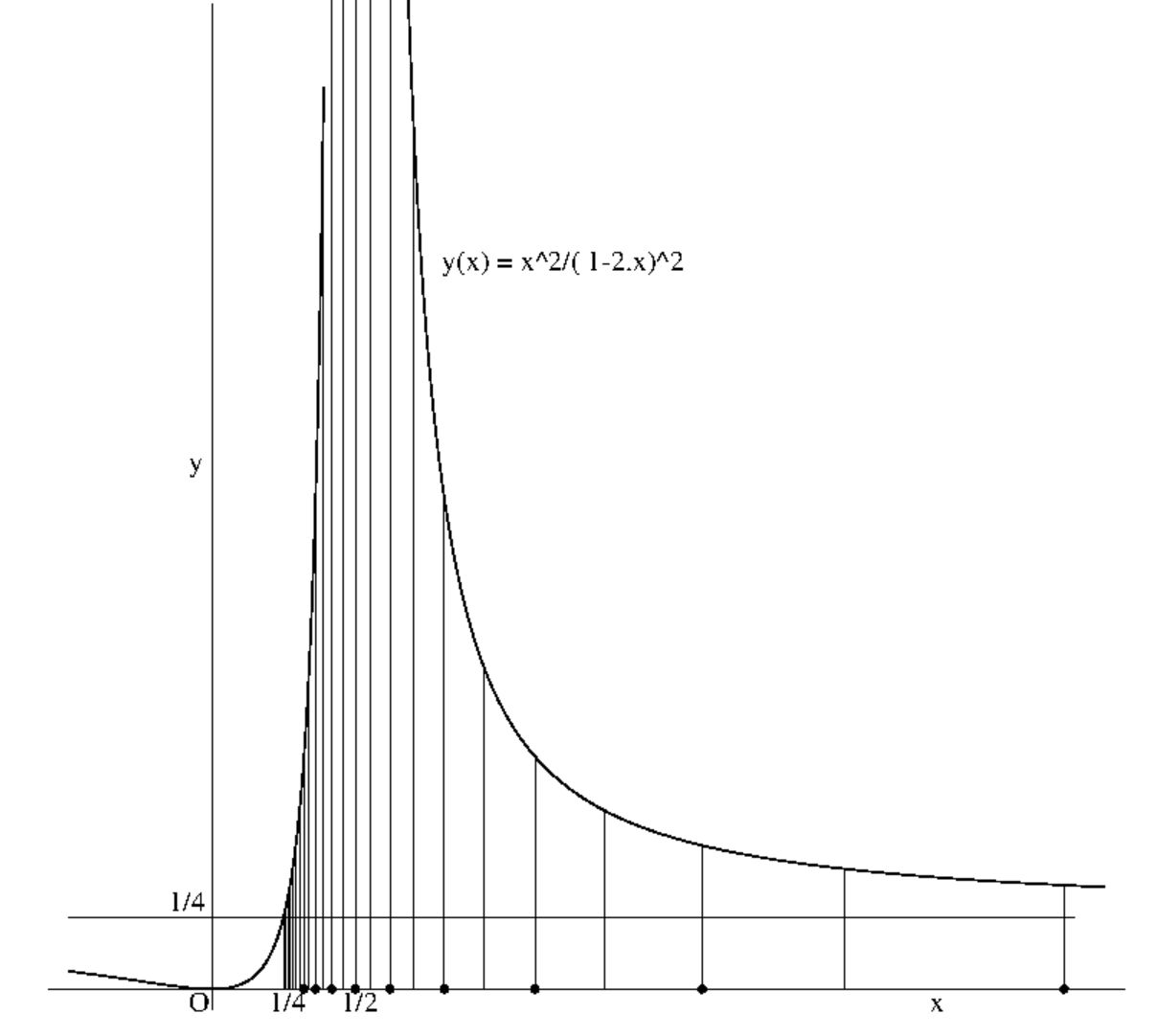
During a coarsening process, points $x$ may give rise to other points $x=y(x)$ which are such that $x$ approaches the value $1/2$, in the end. For this value the denominator $(1-2.x)$ becomes zero. Points $x$ such as mentioned will be called dangerous in the sequel. Let's forget for a moment the somewhat premature discovery that $x<1/3<1/2$. And let the search for dangerous points start here from scratch: $$ x' = \left( \frac{x}{1-2.x} \right)^2 \hieruit \sqrt{x'} = \frac{x}{1-2.x} = \frac{x}{2.x-1} \hieruit $$ $$ \pm \: x = \sqrt{x'} \: (2.x-1) \hieruit x \: (2.\sqrt{x'} \pm 1) = \sqrt{x'} \hieruit $$ $$ x = \frac{ \sqrt{x'} }{ 2.\sqrt{x'} \pm 1} = \frac{1}{2 \pm 1/\sqrt{x'} } $$ Hence each dangerous point will give rise to 2 other dangerous points. After 4 iterations, for example, there will be $1+2+4+8+16 = 31$ dangerous points. It seems useful to know how these points are distributed along the $x$-axis. Some experimental results are depicted in the above figure.
It is conjectured that the whole area $1/4 < x < +\infty$ is, in fact, more or less dangerous, with exception perhaps of a few stationary points. But even for such invariant points, there is always the danger of becoming less stationary, because of roundoff errors. The latter will inevitably be present, as soon as numbers are calculated in a real world environment.
If the above is true, then the only "safe" domain for $x$ while iterating with the function $y(x)$ would be given by $0 \le x \le 1/4$. Better substitute the values $x = a.b$ and $y = a'.b'$. Then we find, indeed, that the denominator will never be zero: $$ 0 \le a.b \le \kwart \hieruit \half \le 1 - 2.a.b \le 1 $$ And we know for sure that $a.b$ will never "escape" from the interval $(0,1/4)$.
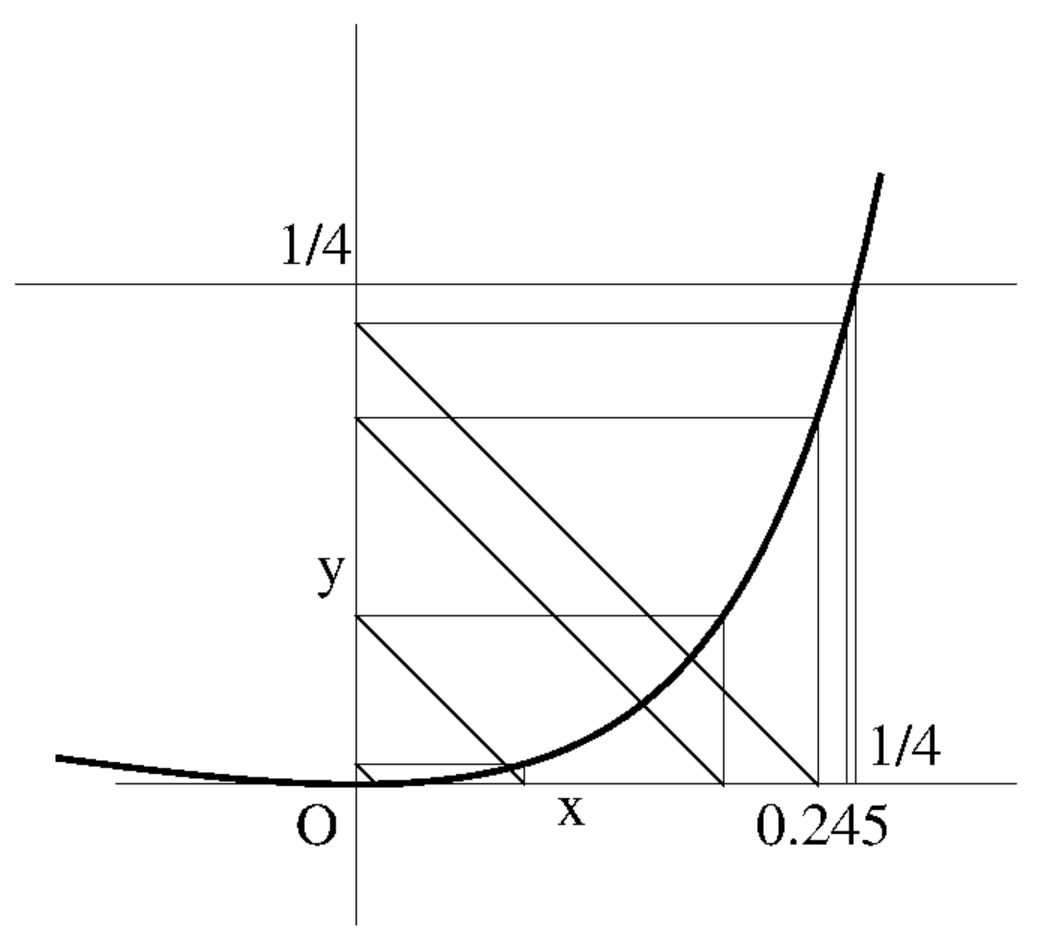
If a starting value of $x = a.b$ is selected somewhere inside the interval $0 \le x < 1/4$, and it does not coincide with the point $1/4$, then it is observed that the successive iterates converge (rather quickly) to $x = 0$. If we commit ourselves to modern terminology, then we would say that the point $x = 0$ is an attractor of the function $y(x) = x^2/(2.x-1)^2$ over the interval $0 \le x < 1/4$. An enlargement of the function in the neighbourhood of the attractor is depicted in the figure below. Click On Pic for viewing the PostScript code:

"Some Stable Solutions" were found in the chapter with the same name, but they were found regardless of any considerations about a "safe" domain of interest. Is it a coincidence that the safety condition $a.b \le 1/4$ does not play any role in this case? Is it perhaps due to the fact that the stability condition we have adopted instead, is actually stronger than the condition for safety? Let's see: $$ a + b \le 1 \hieruit (a + b)^2 \le 1 \hieruit a^2 - 2.a.b + b^2 \le 1 - 4.a.b $$ $$ \hieruit 1 - 4.a.b \ge (a - b)^2 \ge 0 $$ Herewith it is demonstrated that Stability is, indeed, a sufficient condition for Safety. But it should be emphasized, at the same time, that Stability is not necessary for Safety: there may exist Safe Solutions which are not Stable.