Newton-Raphson

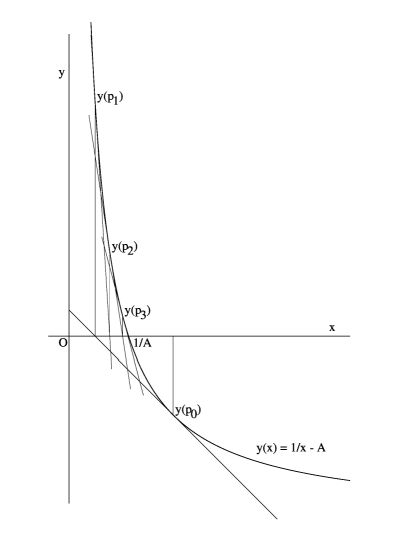
The Newton-Raphson method is a numerical algorithm for finding zeros $p$ of a function $f(x)$. The gist of the method is to draw successive tangent lines and determine where these lines intersect the x-axis (see figure): $$ y - f(p_n) = f'(p_n).(x - p_n) \quad \mbox{where} \quad y = 0 \quad \mbox{and} \quad x = p_{n+1} \quad \Longrightarrow $$ $$ p_{n+1} = p_n - \frac{f(p_n)}{f'(p_n)} $$ Thereby assuming that the whole process will be convergent.
The method can be used for performing a division without actually performing a division. (I found this in a reader about Numerical Analysis.) The equation to be searched for its roots, in this case, is given by: $$ \frac{1}{x} = a $$ Substitute $f(x) = 1/x - a$ in the above algorithm. Resulting in: $$ p_{n+1} = p_n - \frac{1/p_n-a}{-1.1/p_n^2} = p_n - (- p_n + a.p_n^2) \quad \Longrightarrow \quad p_{n+1} = 2.p_n - a.p_n^2 $$ It is well known that the Newton-Raphson method, if it converges, then it does so quadratically, meaning that the inverse $1/a$ can be found rather quickly. The algorithm has been used in the old days, on computers which had no floating point division instruction available. Click On Pic for viewing the accompanying PostScript code of this picture:

Thus by employing the Newton-Raphson algorithm, the inverse of a number can be found with quadratic speed, by performing solely additions and multiplications. Armed with this knowledge, let's make the transition from numbers to matrices. Determining the inverse of a matrix, filled with many numbers, seems to be much more like a challenge anyway.
Let the iterative process for matrices be defined by: $$ P_0 = I \quad \mbox{and} \quad P_{n+1} = 2.P_n - A.P_n.P_n $$ Here $I$ is the unity matrix, $A$ is the matrix to be inverted and $P_n$ are the successive iterands, which should converge to the inverse matrix $A^{-1}$.
An "initial guess" or "preconditioner" $T$ may be chosen instead of the unity matrix $I$. Such a preconditioner $T$ may be equal to the inverse of the main diagonal of $A$, if things are to be kept simple. This effectively means that each row of $A$ (and each element of the right hand side $b$) is divided by the accompanying main diagonal element. The result is a system of equations which is commonly called normed. In a normed system of equations, all elements of the main diagonal are equal to $1$. With other words: the main diagonal is equal to the identity matrix. It is noted that an eventual symmetry of $A$ will be destroyed by carrying out this process of normalization. However, it will be assumed below, for the case of simplicity, that the starting point is just the unity matrix. Hence $T = I$.

Theorem: $$ \mbox{Let} \quad M = (I - A) \quad \mbox{or} \quad A = (I - M) \quad \mbox{then:} \quad P_n = (I - M^{2^n}) . A^{-1} $$ Proof by induction: \begin{eqnarray*} P_0 &=& I = A . A^{-1} = (I - M) . A^{-1} \\ P_{n+1} &=& \left(I - M^{2^{n+1}} \right) . A^{-1} \\ &=& \left(I - M^{2^n.2} \right) . A^{-1} \\ &=& \left[I - (M^{2^n})^2 \right] . A^{-1} \\ &=& \left(I - M^{2^n} \right) . \left(I + M^{2^n} \right) . A^{-1} \\ &=& \mbox{because all matrices are mutually commutative:} \\ &=& \left(I - M^{2^n} \right) . A^{-1} . \left[ 2.I - A.\left( I - M^{2^n} \right).A^{-1} \right] \\ &=& P_n.(2.I - A.P_n) = 2.P_n - A.P_n.P_n \end{eqnarray*} Let $m = 2^n$, then: $$ P_n = (I - M^m) . (I-M)^{-1} $$ For numbers, this would be the sum of a Geometric Series: $$ (I - M^m).(I - M)^{-1} = (I + M + M^2 + M^3 + M^4 + M^5 + M^6 + ... + M^{m-1}) $$ For matrices, this Geometric Series turns out to be equivalent to an iterative "incremental Jacobi" solution method, as will be explained in Appendix I.
But there also does exist a product of terms, called the Euler expansion: \begin{eqnarray*} & (I - M^m).(I - M)^{-1} = (I + M^{m/2}).(I - M^{m/2}).(I - M)^{-1} = \\ & (I + M^{m/2}).(I + M^{m/4}).(I - M^{m/4}).(I - M)^{-1} = \\ & (I + M^{m/2}).(I + M^{m/4}). \, ... \, (I+M^2).(I+M).(I-M).(I-M)^{-1} = \\ & (I + M^{m/2}).(I + M^{m/4}). \, ... \, (I + M^8).(I + M^4).(I + M^2).(I + M) \end{eqnarray*} Let the system of equations to be solved be given by $A.w = b$. Using the above sequences, we can write: $$ P_n = (I - M^{2^n}) . A^{-1} \quad \Longrightarrow \quad A^{-1} b = (I - M^{2^n})^{-1} . P_n b $$ $$ = (I - M^{2^n})^{-1} . (I + M^{m/2}).(I + M^{m/4}). \, ... \, (I + M^8).(I + M^4).(I + M^2).(I + M) b $$ Another way of looking at this is the following: \begin{eqnarray*} & (I-M)^{-1} = (I-M)^{-1}.(I+M)^{-1}.(I+M) = (I-M^2)^{-1}.(I+M) = \\ & (I-M^2)^{-1}.(I+M^2)^{-1}.(I+M^2).(I+M) = (I-M^4)^{-1}.(I+M^2).(I+M) \end{eqnarray*} With other words: $$ w = (I-M)^{-1}.b = (I-M)^{-1}.(I+M)^{-1}.(I+M).b = (I-M^2)^{-1}.(I+M).b $$ Define $b := (I + M).b$ and $M := M^2$. Then again: $$ w = (I-M)^{-1}.b = (I-M)^{-1}.(I+M)^{-1}.(I+M).b = (I-M^2)^{-1}.(I+M).b $$ And this process can be repeated until we find a way to determine $(I-M)^{-1}$, preferrably without continuing the iterations ad infinitum. However, is there any reason to believe that $M^2$ is more amenable, one way or another, than $M$?