Haisch, Rueda, Puthoff

For someone with only a hammer, everything looks like a nail: <quote> I am always very suspicious if somebody tries to explain (too?) many physical systems with one idea - I simply don't believe that this will be possible.</quote>

Key reference is the monograph by Barry Setterfield: Cosmology and the Zero Point Energy (Natural Philosophy Alliance Monograph series, No.1, 2013, ISBN 978-1-304-19508-1).
The most important element in Setterfield's book is the Zero Point Energy (ZPE) or Zero Point Field (ZPF), but it is not an invention of his own (as will be admitted by the author himself, without doubt). Associated with the ZPF are the names of several persons. To mention two of them:

It is thus clear that the whole idea of the Zero Point Field as a Theory of Everything stems from a school, with Bernard Haisch, Harold Puthoff, Alfonso Rueda running the master class.
Bernard Haisch has his own website and he is the director of his own company (not quite a shocking fact these days): What follows is a few snippets from this self-proclaimed "New Physics" (Nieuwe natuurkunde). Let's take a closer look at one of the key papers at the site, written by Haisch, Rueda and Puthoff: It seems that the derivations start with the formulas (2) and (3) in there. According to the Unruh effect, an observer moving with an acceleration $a$ will experience a temperature $T$ associated with black body radiation ($k_B =$ Boltzmann constant). $$ T = \frac{\hbar a}{2\pi c k_B} $$ Note that the Unruh effect has not yet been observed experimentally, though. Whatever. If the Unruh effect assumed to be "real", then Planck's "second law" can be written as: $$ \rho(\omega)d\omega = \left[\frac{\omega^2}{\pi^2 c^3}\right] \left[1 + \left(\frac{a}{\omega c}\right)\right] \times \left[\frac{\hbar \omega}{2} + \frac{\hbar \omega}{\exp(2\pi c\omega/a)-1}\right] $$ And then comes the derivation, it seems. Has it been suggested by some that SED is much simpler than QED? Then take a look at this fragment, please, just one among the many:


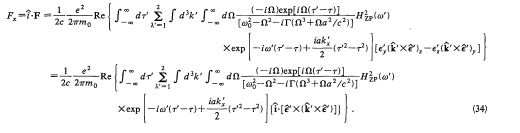
So far so good about the mathematical machinery. Because I'm lazy (sometimes), I had to assume that it is correct. And I've been heading for end results only. This is what I've found.
At page 690 on the left: The ZPF-determined inertial mass associated with the parton oscillator is $$ m_i = \Gamma \frac{\hbar \omega_c^2}{2\pi c^2} \qquad (110) $$ A simple estimate, using this value of $m_i$, as done by Puthoff [2], gives $\omega_c = (2\pi)^{1/2} \omega_P$ where $\omega_P$ is the Planck frequency $\omega_P = (c^5/\hbar G)^{1/2}$ and $G$ is the Newtonial gravitational constant. Hence: $$ m_i = (\Gamma \omega_P)\frac{\hbar \omega_P}{c^2} = \frac{2}{3} \alpha \frac{m_P^2}{m_0} \qquad (111) $$ where $\alpha$ is the fine-structure constant $\alpha=e^2/\hbar c$, and $m_P = \hbar\omega_P/c^2$ is the so-called Planck mass.
At page 690 on the right: The unknown free parameter is, of course, the parton mass $m_0$, or, entirely equivalently, the Abraham-Lorentz damping constant, $\Gamma = 2e^2/3m_0c^2$.
Alright. So what we actually have accomplished in the end is: almost NOTHING. The chain is as weak as its weakest link. And the weakest link is that there is no way to assign a value to $m_0$. If the calculations are correct - let's assume that they are - then all that has been demonstrated is that there exists sort of a quantity $m_i$ that behaves in much the same way as an inertial mass. Interesting perhaps, but without further quantification rather useless.
Remarkably enough, Inertia as a zero-point-field Lorentz force has a more recent successor (2013), which is found in the list of Articles by Bernard Haisch as:

In this paper "the analysis will be done within a formulation that uses nonrelativistic quantum electrodynamics with the creation and annihilation operators rather than the approach of Rueda and Haisch using stochastic electrodynamics". Huh? I've always thought that QED is relativistic by definition. But OK, that's what they say. It is claimed again that the inertial mass is a merely phenomenon caused by the ZPF. But there is more: the equivalence of inertial and gravitational mass is claimed to be a side-effect of the ZPF as well. Whatever. Let's find some end-results. Newton's law $\vec{F} = m_i \vec{a}$ is mimicked aby an analogous formula, where the inertial mass is given by: $$ m_i = \frac{V_0}{c^2}\int\eta(\omega)\frac{\hbar\omega^3}{2\pi^2c^3}d\omega \qquad (29)\\ \mbox{with SED:} \qquad m_i = \Gamma \frac{\hbar \omega_c^2}{2\pi c^2} \qquad (110) $$ The weak link of the chain is "where we now introduce the henceforth frequency-dependent coupling or interaction coefficient $0 \le \eta(\omega) \le 1$". Moreover, what is the volume $V_0$ of the parton? Whatever. Compare this QED result with the SED formula previously found. I would expect some sort of look-alike, but it seems that there is none. Should we conclude then that the SED-QED results are mutually inconsistent? Anyway, I'm not alone in my criticism: Admittedly, that concerns the 1994 (SED) version of the theory.
Basic ideas of Haisch & Puthoff et al. are also found back among Electric Universe adherents, such as Wallace Thornhill in: On page 678 of the 2007 paper it reads, indeed: that Newtonian gravity could be interpreted as a van der Waals type of force induced by the electromagnetic fluctuations of the vacuum, the so-called zero-point fluctuations or zero-point field (ZPF). The Zitterbewegung, another favorite among ZPE adherents, is mentioned in this context as well. There is another paper, at last, where it is claimed that Newton's law of gravitation is caused - of course - by the ZPF: That is, we have a look-alike in formula (31) of the paper: $$ \vec{F} = \vec{r}\frac{G M m}{r^3} $$ But the gravitational constant $G$ is wisely not calculated numerically! Indeed, Coulomb's law for electrostatic forces has the same form. That doesn't mean that gravitation is electrostatics. And the radiation from a light bulb spreads according to an inverse square law as well. Which doesn't mean that a Coulomb is a Lumen.