Planck's Radiation Law

Processing math: 23%

Planck's Radiation Law

From Wikipedia we have

Planck's law

with symbols explained in the reference:

$B_\lambda(\lambda, T) =\frac{2 hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda k_B T}} - 1} \quad \Longleftrightarrow \quad B_\lambda(\lambda, T) =\frac{2 c}{\lambda^4}\frac{\frac{hc}{\lambda}}{ e^{\frac{hc}{\lambda k_B T}} - 1}$ Formulated as such, because there is also a version with the Zero Point Energy

$\;1/2\,hf=\frac{1}{2}\frac{hc}{\lambda}$ involved:

$B_\lambda(\lambda, T) = \frac{2 c}{\lambda^4} \left[\frac{1}{2}\frac{hc}{\lambda} + \frac{\frac{hc}{\lambda}}{e^{\frac{hc}{\lambda k_B T}}-1}\right] = 2 c\left[\frac{k_B T}{hc}\right]^4 k_B T \left[\frac{hc}{\lambda k_B T}\right]^4 \left[\frac{1}{2}\frac{hc}{\lambda k_B T} + \frac{\frac{hc}{\lambda k_B T}}{e^{\frac{hc}{\lambda k_B T}}-1}\right]$ This can be rewritten as follows. Put

$x = (\lambda k_B T)/(hc)$ , then, with a ZPE:

$B_\lambda(x) = (\mbox{scaling factor}) \times \frac{1}{x^4} \left[ \frac{1}{2} \frac{1}{x} + \frac{1/x}{e^{1/x}-1}\right] \sim \left[ \frac{1}{2} \frac{1}{x^5} + \frac{1/x^5}{e^{1/x}-1}\right]$ And without a ZPE:

$B_\lambda(x) \sim \frac{1/x^5}{e^{1/x}-1}$ Where it is noted that there is no singularity in the latter for

$x=0$ , i.e. without the ZPE it holds that

$B_\lambda(0)=0$ :

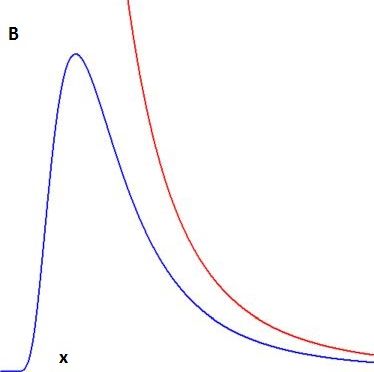
$B_\lambda(0) = \lim_{x\to 0} \frac{1/x^5}{e^{1/x}-1} = \lim_{x\to 0} \frac{1}{x^5\left[1/x + (1/x)^2/2 + (1/x)^3/6 + \cdots\right]} = \\ \lim_{x\to 0} \frac{1}{x^4 + x^3/2 + x^2/6 + x/24 + 1/120 + (1/x)/720 + \cdots} = \\ \frac{1}{0^4 + 0^3/2 + 0^2/6 + 0/24 + 1/120 + \infty/720 + \cdots} = \frac{720}{\infty} = 0$ It is clear that the function

$\color{red}{with}$ the ZPE has a singularity

$\sim 1/2\,(1/0)^5$ for

$x=0$ (ultraviolet catastrophe). This means that it cannot serve as a radiation law. The function

$\color{blue}{without}$ the ZPE is Planck's Radiation Law (apart from scaling factors). The oscillators that are responsible for emitting the radiation actually do have a ZPE, but the black body radiation itself does not have one.

More appropriate for engineering purposes is the Stefan-Boltzmann law of radiation:

$u = a T^4 \quad \mbox{with} \quad a = \frac{4\sigma}{c}$ Where

$u=$ energy density,

$T=$ absolute temperature (

$K$ ) and

$\sigma = 5.73 \times 10^{-8} W/m^2/K^4$ is the Stefan-Boltzmann constant. With formula (288) in The Theory of Heat Radiation, the radiation density constant

$\,a\,$ is expressed in other constants as:

$u = a T^4 = \frac{8\pi^5}{15}\frac{(kT)^4}{(hc)^3}$ Where it is typical that Max Planck clearly hasn't been aware of the following mathematical fact:

$1 + \frac{1}{2^4} + \frac{1}{3^4} + \frac{1}{4^4} + \cdots = \frac{\pi^4}{90}$ However. It's important to realize that Black Body Radiation actually doesn't exist, at all, in reality. It's a mathematical model, an idealization, much like for example the ideal pendulum. Heat radiation in reality is not black: it's grey. Strictly speaking, there exist no physical bodies that can literally absorb all radiation impinging on them, which would be the proper definition of a perfect black body. So let's give a quick overview of a more "realistic" approach in the theory of Heat Radiation. It is an idealization as well, though, as is common with any mathematical modelling of physical reality.

Radiative heat transfer is always between two bodies $(i,j)$ with a temperature difference. In general, the flow of heat between $(i)$ and $(j)$ has the form: $Q_{j\rightarrow i} = \sigma\cdot A_{i,j}\left(Tj^4-T_i^4\right)$ Where:

$\sigma =$ Stefan-Boltzmann constant (see above)
$A_{i,j} =$ factor with dimension of area $[m^2]$ , dependent on emission coefficients, radiative areas and, last but not least: View factors.
$T =$ (absolute) temperature ( $K$ )

There is a Wikipedia reference about all this.
The heat flow can be written as the admittance

$\gamma_{i,j}$ of a resistor, times the temperature difference:

$Q_{j\rightarrow i} = \gamma_{i,j}\left(Tj-T_i\right)$ Where the admittance - though linearized reasonably well - is still dependent on the temperatures:

$\gamma_{i,j} = \sigma\cdot A_{i,j}\left(Tj^2+T_i^2\right)\left(Tj+T_i\right)$ So iterations may be necessary, but the hard part is in

$A_{i,j}$ and the view factors, most of the time.

Planck's Radiation Law

Planck's law