The Casimir Effect

Key reference is the monograph by Barry Setterfield: Cosmology and the Zero Point Energy (Natural Philosophy Alliance Monograph series, No.1, 2013, ISBN 978-1-304-19508-1).

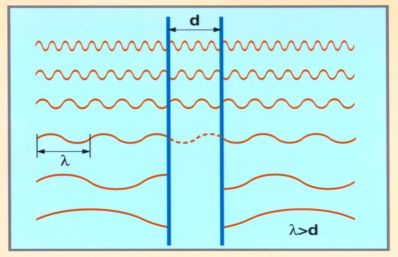
Figure 3: The Casimir Effect. The two vertical blue lines represent the two parallel metal plates in a vacuum. The distance the plates are apart is $d$ . The top three series of waves have wavelengths, $\lambda$ , which are short enough to fit exactly between the plates. The bottom two series of waves have wavelengths greater than $d$ , and so do not fit between the plates. This bottom two series of waves exert pressure on the plates which pushes them together. The wave series third from bottom has the largest wavelength that will fit exactly between the plates. All longer waves are excluded and exert a pressure from the outside.

Upon careful inspection of Figure 3 on page 39 and reading carefully the caption below it, it should be clear that Setterfield doesn't quite understand the ins and outs of the effect:

Indeed, one favorite argument among adherents of the Zero Point Energy field in vacuum is the Casimir effect. However, what is being revealed when reading the Wikipedia page carefully? The effect is explained solely by considering electromagnetic waves, that is: photons, light. Apart from any theoretical considerations, as far as I can see, the Casimir effect is one of the very rare more or less direct experimental evidence for a ZPE in vacuum. Bad news though: it assumes the a priori existence of photons, i.e. light waves. Consequently, the ZPE cannot serve as a suitable explanation for e.g. a variable light speed, for the simple reason that it presumes a photon production in the vacuum, which is light itself. This is one of the loopholes in Setterfield's Theory of Everything. There are no virtual particle pairs of some sort other than photons. And these are not produced as particle - antiparticle pairs, one particle having a positive (+) and the other having a negative (-) charge, because photons have no charge. Whatever. The total (mean) Zero Point Energy calculated is an infinite (but hopefully constant) contribution plus the following: $$ E_{ZPE} = \infty + \frac {\hbar\,c\,\pi^2} {3\times240\,d^3} $$ Apart from the infinity, here we have another problem. According to Setterfield's theory, the Zero Point Energy is changing with cosmic time. But, according to the same theory, the product of Planck's constant and the speed of light does not change: $h\,c =$ constant. It must be concluded from the latter that $E_{ZPE}$ does not change either, in blatant contradiction with the statement that the Zero Point Energy does change.
Anyway, the end result of the calculations is a testable prediction: $$ {F_c \over A} = -\frac {\hbar\,c\,\pi^2} {240\,d^4} = -\frac{\pi\,h\,c}{480\,d^4} $$ with $F_c =$ Casimir force, $A =$ area of the plates, $\hbar =$ reduced Planck constant, $c =$ speed of light (!!) , $d =$ distance between the plates. There are two details in the Wikipedia derivation that I find suspect. Renormalization of the infinities in the first place, of course, which seems to be virtually inevitable with QuantumElectroDynamics (QED). But another issue is this: $$ \langle E \rangle = \frac{\hbar}{\color{red}{2}} \cdot \color{red}{2} \int \frac{A\,dk_x\,dk_y}{(2\pi)^2} \sum_{n=1}^\infty \omega_n $$ Where it is said that "a factor of 2 is introduced for the two possible polarizations of the wave". Thus annihilating the factor $1/2$ which is so typical for the Zero Point Field. Doesn't that simply mean that, instead of ZPF waves, ordinary photons with energy $\,\hbar\omega_n\,$ have come into play? (Just a honest question: I'm not an expert on this)
In order to be able to observe the effect, the plates must be metallic. Confirming that the physical phenomenon involved must be of an electromagnetic nature. Electromagnetic radiation, to be precise. This is clear from the theoretical derivation and from the fact that the speed of light $\,c\,$ is part of the Casimir force formula. Now electromagnetic radiation is the same as photons. But how can photons have an energy $\,\hbar\omega/2$ ? Would it mean that half photons can be created in the vacuum? So far so good for the Wikipedia derivation.
Admittedly, QED has come up with a no-nonsense result that can be tested experimentally, given sufficient technology and human effort. How about SED? Does it calculate the Casimir effect equally well? And without the infinities, preferably? What I have found is a reference, in Dutch, where on page 14 there is a calculation of the effect: It is claimed that this calculation is done with Stochastic Electro Dynamics (SED). But I cannot see much difference with the QED derivation in the first place. And infinities are not removed with SED in the second place, as uttered explicitly on page 16. If the continuum approach is replaced by discrete mathematics, based upon a grid with Planck lengths, then there still is an an immense outcome for the Zero Point Energy, which is virtually impossible to match with reality. As is actually the final conclusion of the paper.

Dimensional analysis

A simple and straightforward derivation of the Casimir force, though somewhat incomplete, can be accomplished with help of Dimensional analysis. Assume that the phenomenon is quantum mechanical and electromagnetic, meaning that the Planck constant $h$ and the Speed of light $c$ shall be involved. Then the Casimir pressure, which is the force $F_c$ divided by the area $A$ of the plates, together with the distance $a$ between the plates, can be written as: $$ F_c/A = (h)^\alpha \times (c)^\beta \times (d)^\gamma $$ When expressed in metric units: $$ kg \cdot m \cdot s^{-2} \cdot m^{-2} = (kg\cdot m^2\cdot s^{-1})^\alpha \times (m\cdot s^{-1})^\beta \times (m)^\gamma \quad \Longrightarrow \\ kg \cdot s^{-2} \cdot m^{-1} = kg^\alpha \cdot s^{-\alpha-\beta} \cdot m^{2\alpha+\beta+\gamma} $$ From which it follows that: $$ \alpha = 1 \quad ; \quad \beta = 1 \quad ; \quad 2\alpha+\beta+\gamma = 2+1+\gamma = -1 \quad \Longrightarrow \quad \gamma = -4 $$ Consequently, without any constants, without a plus or a minus sign, but nevertheless in concordance with the more complete result: $$ \frac{F_c}{A} \sim \frac{h\,c}{d^4} $$

1-D Renormalization

Singularities form a nasty issue, whether that is with QED or with SED. Therefore we shall devise the mathematical model of a non-existent Casimir effect, namely in one-dimensional space. And explore the consequences. The advantage is that perhaps we finally are going to understand what Renormalization is all about. Some elements of the model are found in a Wikiversia page.
Electromagnetic waves inside the plates are all subject to the boundary condition that their amplitude is zero at the plates. They form standing waves inside and have resonant frequencies. The distance $d$ between the plates hence must be a number $k$ of times half the wavelength $\lambda$: $$ d = k\,\frac{1}{2}\lambda \quad\Longrightarrow\quad \lambda = 2\,d/k $$ For the energy $E$ of one photon we calculate, with $T =$ period and $\nu =$ frequency: $$ \lambda = c\, T = c/\nu \quad\Longrightarrow\quad \nu = \frac{c}{2\,d/k} \quad\Longrightarrow \\ E = h\,\nu = \frac{h\,c}{2\,d}\,k \quad \mbox{with} \quad k=1,2,\cdots\,,\infty $$ So far so good for the waves inside the plates. Now is is reasonable to assume that the waves / photons outside the plates have continuous instead of discrete energies: there is no resonance there. Let us write, with $\,x\,$ being a continuous variable ranging from zero to infinity: $$ E = h\,\nu = \frac{h\,c}{2\,d}\,x \quad \mbox{with} \quad 0\le x \le \infty $$ In order to calculate the total energy inside as well as outside the plates, the energies inside must be summed and the energies outside must be integrated: $$ E_\mbox{inside} = \sum_{k=0}^\infty \frac{h\,c}{2\,d}\,k\times 1 \quad ; \quad E_\mbox{outside} = \int_{x=0}^\infty \frac{h\,c}{2\,d}\,x\,dx $$ It should be noticed that we are using the same "scaling" factor $hc/2d$ for both the energies. Because it is expected that they must be in some sense comparable: the only difference being that photons inside are at resonance while photons outside are not. Anyway, it is clear that the energies thus formulated cannot be calculated, because they give rise to infinite outcomes: $$ E_\mbox{inside} \sim \sum_{k=0}^\infty k = \infty \quad ; \quad E_\mbox{outside} \sim \int_{x=0}^\infty x\,dx = \infty $$ That's how Reormalization comes into play. Let us assume that the energy of a photon cannot increase indefinitely and that the higher energies are damped somehow. Usually an exponential function is employed for this purpose. Let the damping constant be named $\,\alpha$ : $$ E_\mbox{inside} = \frac{h\,c}{2\,d} \sum_{k=0}^\infty k\,e^{-\alpha\,k} \quad ; \quad E_\mbox{outside} = \frac{h\,c}{2\,d} \int_{x=0}^\infty x\,e^{-\alpha\,x}\,dx $$ Later on, it will be assumed that the damping constant is very small. Even stronger: we shall calculate the limit for $\,\alpha\to 0$ . This effectively means that $\,e^{-\alpha\,x}\to 1\,$ and we have thus calculated sum and integral without the assumption that there is any damping! Whatever. For the time being, both the sum and the integral can be calculated. The sum is the derivative of a geometric series: $$ \sum_{k=0}^\infty k\,e^{-\alpha\,k} = - \frac{d}{d\alpha} \sum_{k=0}^\infty \left(e^{-\alpha}\right)^k = - \frac{d}{d\alpha} \left(\frac{1}{1-e^{-\alpha}}\right) = \frac{e^{-\alpha}}{\left(1-e^{-\alpha}\right)^2}\\ = \frac{1}{\left(e^{+\alpha/2}-e^{-\alpha/2}\right)^2} = \frac{1/4}{\sinh^2(\alpha/2)} $$ And the integral is: $$ \int_{x=0}^\infty x\,e^{-\alpha\,x}\,dx = - \frac{1}{\alpha} \int_{x=0}^\infty x\,d\left(e^{-\alpha\,x}\right) = - \frac{1}{\alpha} \left\{ \left[ x\,e^{-\alpha\,x} \right]_{x=0}^\infty - \int_{x=0}^\infty e^{-\alpha\,x}\,dx \right\}\\ = - \frac{1}{\alpha} \left\{ - \frac{1}{\alpha} \left[e^{-\alpha\,x}\right]_{x=0}^\infty \right\} = \frac{1}{\alpha^2} $$ The net force on the plates is caused by the difference between the outside and the inside energy, which thus must be calculated first: $$ E_\mbox{outside} - E_\mbox{inside} = \frac{h\,c}{2\,d} \left[ \frac{1}{\alpha^2} - \frac{1}{\left(e^{+\alpha/2}-e^{-\alpha/2}\right)^2} \right] $$ With help of a Computer Algebra System (MAPLE), we find a serie expansion for the inside energy term: 
> series(1/(exp(x/2)-exp(-x/2))^2,x);

               -2                 2           4      5
              x   - 1/12 + 1/240 x  - 1/6048 x  + O(x )
Consequently: $$ E_\mbox{outside} - E_\mbox{inside} = \frac{h\,c}{2\,d} \left[ \frac{1}{\alpha^2} - \left\{\frac{1}{\alpha^2} - 1/12 + 1/240\;\alpha^2 - 1/6048\;\alpha^4 + \cdots \; \right\}\right] $$ It has been assumed that the damping constant $\alpha$ is very small. In order eliminate it, we calculate the limit. This results in the Casimir Energy $E_c$ of our one-dimensional model: $$ E_c = \lim_{\alpha\to 0} \left[E_\mbox{outside} - E_\mbox{inside}\right] = \frac{h\,c}{2\,d} \left[ 1/12 - 1/240\;\alpha^2 + 1/6048\;\alpha^4 - \cdots \; \right] = \frac{h\,c}{24\,d} $$ Remember that energy $=$ work $=$ force $\times$ path $d$. So, at last, the one-dimensional Casimir force $F_c$ is the derivative to $d$ of the above total energy difference: $$ F_c = \left[\frac{h\,c}{24\,d}\right]'_d = - \frac{h\,c}{24\,d^2} $$ A result which is not contradictory to $\,F_c/A \sim h\,c/d^4$ , though it seems so at first sight, because in one dimension there doesn't exist such a thing as an area $\,A\,$ and the dimensionality of $\,d^4/A\,$ and $\,d^2$ is nevertheless the same.

Another attempt

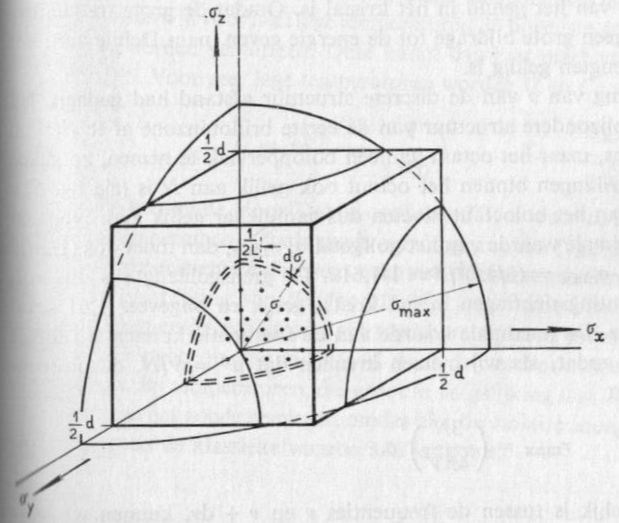
Let's assume for a moment that Setterfield's approach is correct and that only electromagnetic waves with wavelength greater than the distance between the plates are responsible for the Casimir effect. From Leerboek der natuurkunde by R.Kronig, 7th edition on page 700 then we have a theory by Debije. According to this theory, the number of possible vibrations between $\nu$ and $\nu+d\nu$ is found by counting the number of discrete points in $\sigma$-space between $\sigma (=\nu/c)$ and $\sigma+d\sigma$. All these points are within the octant of a spherical shell with radius $\nu/c$ and thickness $d\nu/c$, with volume $(4\pi/8)(\nu/c)^2d\nu/c$. In $\sigma$-space there is one point in a volume of $(1/2L)^3=1/8V$, hence the number of points in the spherical shell and hence the number of vibrations between $\nu$ and $\nu+d\nu$ is equal to: $$ \frac{4\pi\nu^2d\nu}{8c^3}/ \frac{1}{8V} = \frac{4\pi V}{c^3}\nu^2d\nu $$ The total Zero Point Energy is found to be: $$ E_c = \int_0^{\nu_{max}} h\nu \frac{4\pi V}{c^3}\nu^2d\nu = \frac{4\pi h V}{c^3}\frac{1}{4} \nu_{max}^4 = \frac{\pi h A d}{c^3} \left(\frac{c}{2d}\right)^4 = \frac{\pi h A c}{16 d^3} $$ And the Casimir pressure is: $$ F_c/A = - \frac{\pi\,h\,c}{16/3\, d^4} \ne -\frac{\pi\,h\,c}{480\,d^4} $$ To be honest, I find all of the above calculations quite slippery; it feels like walking on thin ice. What's worse, there exist references contradicting the validity of them:

Most other references, though, are in favour of the Zero Point Energy hypothesis:
Other articles by Gerold Gründler are at the website Astrophysical Institute Neunhof and elsewhere: