Square Bubbles

The current section will be about mathematical models. As an introduction to the subject, the Square Bubbles anecdote is relevant. The story contains some mathematical details. And these are essential. The reader is invited not to skip the one or two formulas in this presentation. Technically, the matter is simple enough to be understood on the basis of little more than high school knowledge.
Many years ago - being a fourth year student at the Eindhoven University of Technology (Technische Hogeschool Eindhoven at that time) - I was faced with the following problem. And to be honest, I was not able to find a good way to tackle it, let alone to solve it. Oh yes, all sort of complicated formulas about tensors on curved surfaces were developed, resulting in my private "fundamental bubble theory", that turned out to be entirely besides the point.

Abstraction

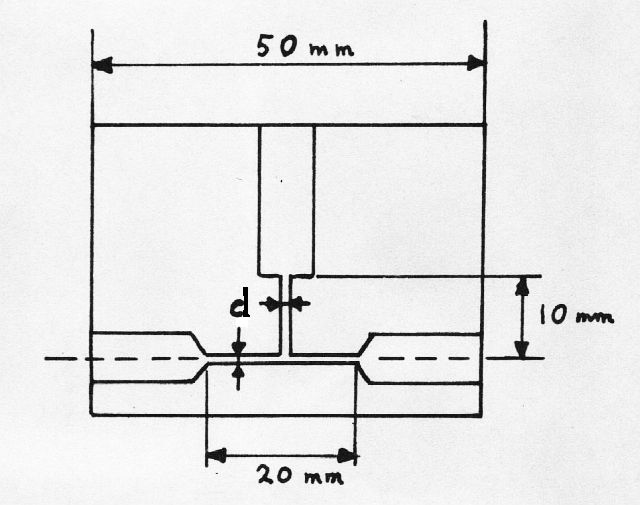
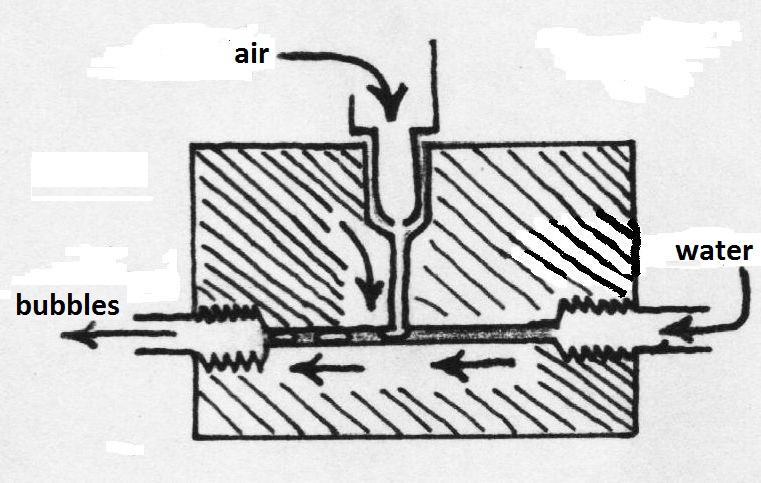
Given a piece of perspex with two capillary tubes in it, joined together in the form of a T. Water flows from the right to the left through the horizontal tube. Air flows from the top to the bottom through the vertical tube. Where the two media meet, formation of bubbles takes place. This mixture of air and water (bubbles) flows out through the horizontal tube. The diameter of the capillaries is 1.0 mm.

Independent variables are the volume flows of air and water, also called air flow $F_L$ and water flow $F_W$. Dependent variables are the frequency $f$ of the bubbles and the bubble volume $V_L$. (It is theoretically possible, but not very practical to consider instead the volume of "water bubbles" $V_W$.) As can be easily shown, there is a simple relationship between the frequency and the bubble volumes: $V_L = F_L/f$ and $V_W = F_W/f$.
The intention has been to also determine experimentally whether there exists a relationship between the independent and dependent variables. Meanwhile we know that such measurement is a form of Abstraction. The measured values are shown in the table below. The value marked with (*) was originally 1.9, which most likely is based on a writing error during the measurements.

Air (mm3/s) Water (mm3/s) Frequency (1/s)
44 56 31
62 50 35
66 45 35
78 45 37
140 41 43
149 42 44.5
29 70 25
18 79 20
9 98 14.5
6 133 11
21 177 42
18 180 35
14 199 30
7 205 19 *
9 232 22
1 235 2.4
33 145 47
49 135 57
55 135 62
62 124 60
66 117 65
91 117 80
95 152 80
96 109 75
99 108 73
120 112 90
122 92 76
145 115 92
146 98 88
157 98 97
169 100 95

Subsequently it was expected that I should be able explain the measurements, by devising a mathematical model. The phenomenon of bubble formation has been put on film as well, in order to be able to study it better. The following pictures are snapshots from that film.

Series 1

Series 2

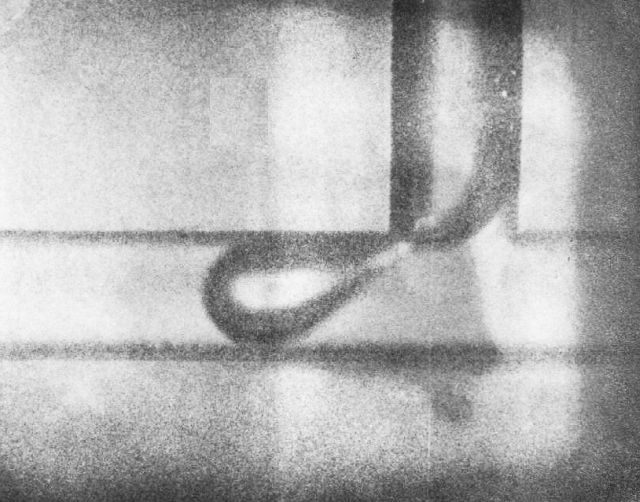
Series 3

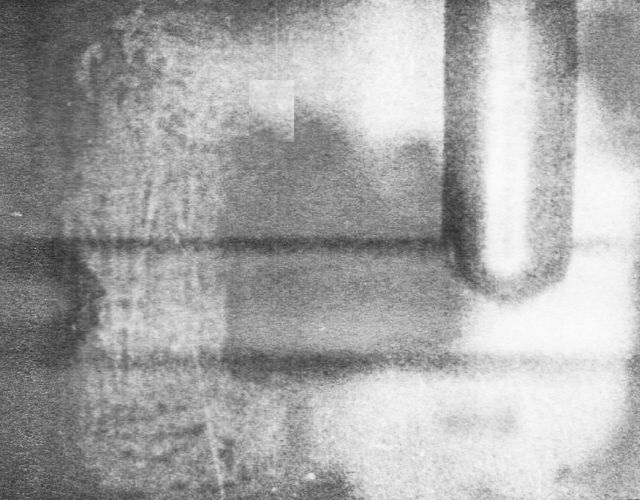
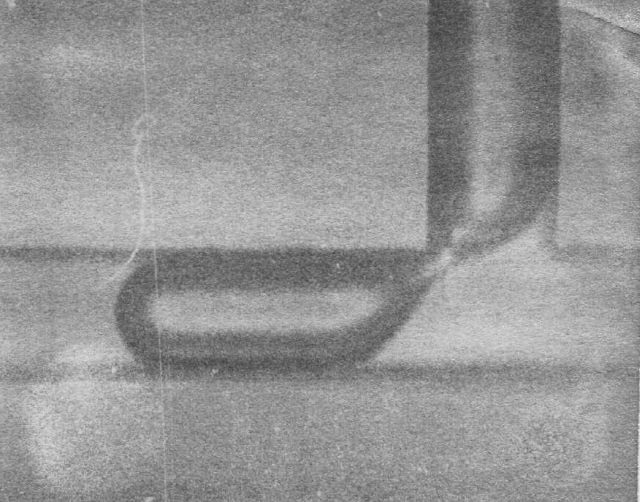
Idealization

After seeing the movie, a friend and fellow student of me, in 5 minutes, solved the whole problem, while sitting with me in the local student's pub, and using the back side of a "coaster" (: thanks to everybody on the Web, for rendering our Dutch "bierviltje" in English). Jacques Staal (1948-2014), he made a few assumptions that simplified the whole problem dramatically.
In retrospect, I am certain that he must have understood perfectly well what is essential and what not with designing a mathematical model. Let us start but assume that the formation of the air bubbles is completely independent of the surface tension, and thus independent of any possible curvature of the surfaces. Then it is in fact not so important what exactly the form the bubble surface is (such in stark contrast to what I had always thought).
The following is a sketch of the T-piece, containing the more "accurate" image of a growing bubble, as seen from one side:

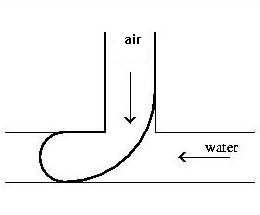
When the bubbles are not required to be round, then we can imagine for our convenience that they are instead, please do not panic: square. This now seems to be the crucial step. It is clear that it is impossible to come to this without a good dose of imagination and without moving away from direct experience.
What is happening here is beyond the ability of a simple measuring instrument. And the solution requires a minimum of physics knowledge. What is really needed, however, is some kind of engineering ingenuity, and quite some guts. In short: a human being is needed here. We can no longer speak of abstraction, we must talk about the creation of an idea in someone's mind: Idealization. An idealized scenario for the formation of bubbles in the T-piece can now be set up. According to the model, it works as shown here:

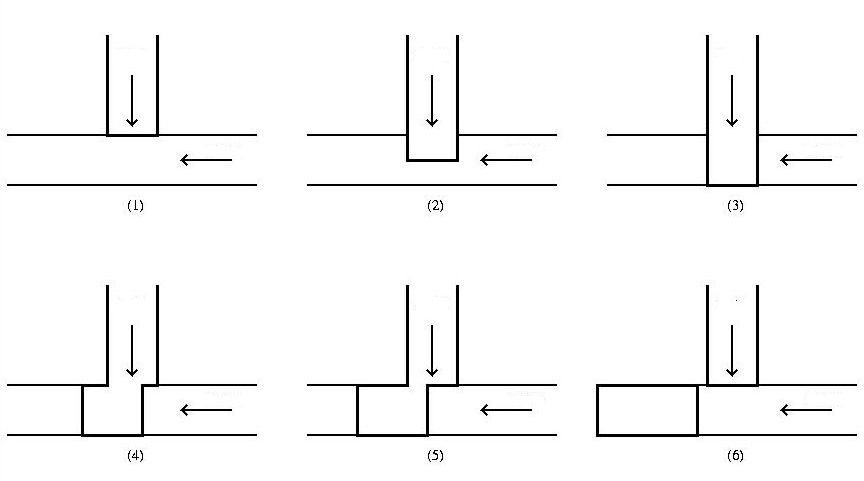
So the idea is that first the bubble is pressed by the air flow against the other side of the water channel (stage 1-3), and then by the water flow across the width of the air duct is cut off (phase 4-6). On the basis of this idealized picture it is possible to set up a meaningful calculation: Or: $\;t_{1-3} = d/(F_L/A)\;$ and $\;t_{4-6} = d/(F_W/A)\;$ . Giving: $\;t_{1-3} = V_0/F_L\;$ and $\;t_{4-6} = V_0/F_W\;$ .
Here: $A =$ flow area, $d =$ channel diameter. Therefore $V_0 =$ sort of "initial" volume, where $V_0 = A.d$ .
The total time needed for bubble formation is : $\;t_{1-6} = t_{1-3} + t_{4-6} = 1/f = V_0 ( 1/F_L + 1/F_W )$ .
Hence the volume of the air bubbles is calculated by: $$ V_L = F_L/ f = V_0 ( 1 + F_L/F_W ) \qquad \mbox{: MATHEMATICAL MODEL !} $$ The only yet unknown quantity in this formula is the initial volume $V_0$ . This "initial volume" can be determined in two independent ways. The first way is based on a rough estimate: the volume must be something in between a sphere and a cylinder.
Given the fact that the diameter of the capillaries is $1$ mm, we find for the cylinder: $\pi/4.d^2.d = 0.785$ . And the sphere: $\pi/6.d^3 = 0.52$ . Hence: $0.52 < V_0 < 0.78$ .
Secondly, we can try to match the the model with the measurements. Let $x=F_L/F_W$ and $y=V_L$. A least squares adjustment gives: $$ \sum_{i=1}^{N} \{V_0 [1 + x_i] - y_i \}^2 = \mbox{minimal} $$ where $N$ is the number of measuring points. This is a quadratic function in $V_0$: $$ A V_0^2 - 2 B V_0 + C = \mbox{minimal} $$ With: $ A = \sum_{i=1}^{N} (1+x_i)^2 $   ;   $ B = \sum_{i=1}^{N} (1+x_i) y_i $   ;   $ C = \sum_{i=1}^{N} y_i^2 \; $ . It is well known that the minimum of this parabola, with $V_0$ as an independent variable, is found for : $V_0 = B/A$ . Or: $$ V_0 = \frac{\sum_{i=1}^{N} (1+x_i) y_i}{\sum_{i=1}^{N} (1+x_i)^2} $$ This gives from the measurements a value of $V_0 = 0.6934510 \approx 0.7 \, mm^3$ : the experimental value is indeed in between the rough theoretical values.

It does matter

Finally the measurements and calculations are put together in a chart. Then we see among other things that the measurements for the smallest bubble volumes systematically deviate from the calculations. This can be explained by the fact that with a more powerful water flow the bubbles rather are "nipped in the bud", which is before their initial volume $V_0$ is reached.

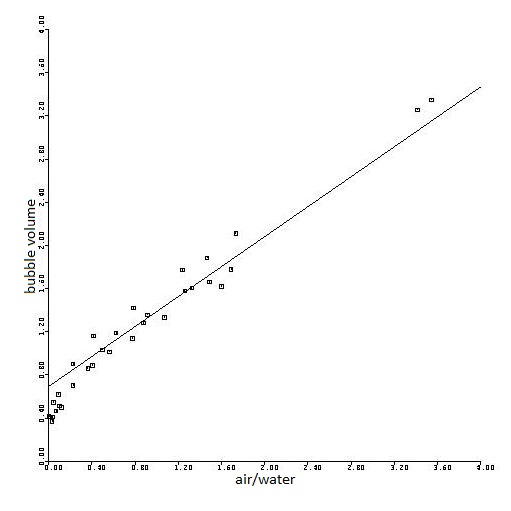
We have derived the fundamental natural law for the formation of bubbles in a T-piece: $V_L = V_0 (1 + F_L/F_W)$. A law that convinces by simplicity and elegance. There's a certain charm associated with such formulas, people say, and one wonders what the the deepest ground is of this charm. In case of the bubbles the answer is clear: the beauty of the formula found is due only to the dramatic simplification that we have applied. The beauty does not occur because we have grasped the reality in all its details, but precisely because we have dispensed of most aspects of reality, not because we have pursued the whole truth, but precisely because we have not pursued that truth. The paradox is that we nevertheless have come closer to "the truth". After all, the result is quantitative, agrees well with the experiments, in short: is exactly what one would expect of a (small) piece of science.

Why so much attention has been given to a relatively inane application like this one? Yes, I did talk about the fundamental law of physics for the formation of bubbles in a T-piece, but that will no doubt be intended as a metaphor. This author certainly is not going to say that a formula for silly bubbles, nice as it is, has the same status as, for example, the Laws of Newton, or the Lorenz Transformations? On the contrary; that's precisely what this author intends to say. One of my key points is that, as one gets deeper about it, no substantial distinction can be made between "fundamental" and "applied" research. If we are a bit further, I will gradually show that this distinction is increasingly difficult to sustain, and finally has to go away. Albeit one can defend that $\,F = m\cdot a\,$ has a broader scope than $\,V_L = V_0 (1 + F_L/F_W)$ , and in that sense is more fundamental. But I will keep my stand that it refers to a gradual, not to an essential difference:

The beauty of "real" natural laws is based on an illusion as well. It is merely the result of a simplification, a simplification that, whether or not deliberately, is applied by us people themselves, and which essentially is distorting reality rather than including it.