Merk op dat het uitsmeer effekt van de tast-funktie des te voelbaarder is naarmate de gemeten funktie $f$ ter plaatse minder "netjes" is. Het is belangrijk om dit te onthouden.
In het algemeen zal men in het midden laten welke van de vijf zinnen bij het
waarnemen van een funktie wordt ingezet. Dit komt tot uiting in de nu volgende
werk-definitie.
De zin $\tilde{f}$ van een reële funktie $f$ is:
$$ \tilde{f}=\lim_{h \rightarrow 0}\int_{-\infty}^{+\infty}\!D(t,h)f(x-t)\,dt$$
Spreek bijvoorbeeld uit als: "$\tilde{f}$ is $f$ in de zin van $D$".
Hierin is de filter D(x,h) een "tast" funktie met de volgende eigenschappen:
$$ \int_{-\infty}^{+\infty}\!D(t,h)\,dt=1 \quad ;
\quad \lim_{h \rightarrow 0} D(x,h) = 0 \quad \mbox{voor alle} \; x \neq 0 $$
Met andere woorden: de tast-funktie konvergeert naar de delta-funktie.
De precieze keuze van de tast-funktie is daarom in feite niet erg belangrijk.
Voorbeelden van tast-funkties:
$$ D1(x,h)=\left\{ \begin{array}{ll}
1/h & \mbox{voor}\;\; -\frac{1}{2}h < x < +\frac{1}{2}h \\
0 & \mbox{voor}\;\; x<-\frac{1}{2}h \;\; \mbox{of} \;\; x>+\frac{1}{2}h
\end{array} \right. $$
$$ D2(x,h)=\frac{h/2\pi}{\left(x^2+h^2\right)^{3/2}} \quad ; \quad
D3(x,h)=\frac{h/\pi}{\left(x^2+h^2\right)} \quad\mbox{: Wazige Optiek} $$
$$ D4(x,h)=\frac{1}{h\sqrt{2\pi}} e^{-x^2/2h^2} \quad
\mbox{: OperatorenRekening}
$$
Gebruik vooreerst de eenvoudigste tast-funktie; dat is $D1$. Dan is:
$$ \tilde{f}(x,h) = \int_{x - \frac{1}{2} h}^{x + \frac{1}{2} h} \, f(t) \, dt \, / h =
\int_{- \frac{1}{2} h}^{+ \frac{1}{2} h} \, f(x - t) \, dt \, / h $$
Ontwikkel $f$ in een Taylor-reeks, als volgt:
$$ f(x-t) \approx f(x) - f'(x).t + f''(x). \frac{1}{2} t^2 \qquad \Longrightarrow $$
$$ \int_{- \frac{1}{2} h}^{+ \frac{1}{2} h} \! f(x - t) \, dt \approx
f(x).h - f'(x).0 + f''(x).\frac{1}{2} \frac{1}{3} 2 \left( \frac{1}{2} \right)^3
\qquad \Longrightarrow $$
$$ \tilde{f}(x) \approx f(x) + \frac{1}{24} h^2 f''(x) $$
Deze formule is geldig voor "nette", continue en differentieerbare funkties.
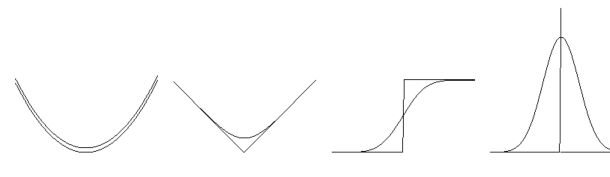
Nemen we bijvoorbeeld de funktie $f(x)=x^2$, dan krijgen we een parabool die
iets naar boven verschoven is:
$$ \tilde{x}^2 = x^2 + \frac{1}{12} h^2 $$
Gebruiken we in plaats van $D1$ de Gauss-funktie $D4$, dan komt er eenvoudig:
$$ \tilde{x}^2 = x^2 + h^2 $$
Als volgende voorbeeld nemen we een funktie die een "knik" heeft, namelijk $ f(x) = |x| $, of uitgeschreven: $$ f(x)=\left\{ \begin{array}{ll} - x & \mbox{voor} \;\; x \leq 0 \\ + x & \mbox{voor} \;\; x \geq 0 \end{array} \right. $$ Omdat de funktie differentieerbaar is in dat gebied vinden we $$ \mbox{voor} \; x < - \frac{1}{2} h \; \mbox{ en voor} \; x > + \frac{1}{2} h \; : \; \tilde{f}(x) = |x| $$ In de buurt van de knik moeten we wat voorzichtiger zijn, dat is voor $ - \frac{1}{2} h < x < + \frac{1}{2} h $ : $$ \frac{1}{h} \int_{x - \frac{1}{2} h}^{x + \frac{1}{2} h} \, f(t) \, dt = \frac{1}{h} \left[ \int_{x - \frac{1}{2} h}^0 (- t) \, dt + \int_0^{x + \frac{1}{2} h} (+ t) \, dt \right] = $$ $$ \frac{ \frac{1}{2} (x - \frac{1}{2} h)^2 + \frac{1}{2} (x + \frac{1}{2} h)^2 }{ h } = \frac{ x^2 }{ h } + \frac{1}{4} h $$ Dit is een stuk van een parabool, met een dal ter waarde $ h/4 $ in $x=0$. Inderdaad is voor $ x = \pm \frac{1}{2} h : \tilde{f}(x) = \frac{1}{2} h $. De parabool sluit netjes aan op de rest van de afgetaste funktie $\tilde{f}$. Gebruiken we in plaats van $D1$ de Gauss-funktie $D4$, dan komt er uiteindelijk: $$ \tilde{f}(x) = \frac{1}{h \sqrt{2 \pi}} \left[ 2 x \, \int_0^x e^{- \frac{1}{2} t^2 / h^2 } \, dt \, + \, h^2 e^{- \frac{1}{2} x^2 / h^2 } \right] $$ Ook deze funktie konvergeert voor $x \rightarrow \pm \infty$ netjes naar $|x|$.
Beschouw nogmaals de Heaviside of sprong-funktie, van dichterbij als toen we de stelling van Brouwer behandelden: $$ f(x)=\left\{ \begin{array}{ll} 0 & \mbox{voor} \;\; x < 0 \\ 1 & \mbox{voor} \;\; x > 0 \\ \frac{1}{2} & \mbox{voor} \;\; x = 0 \end{array} \right. $$ Wanneer we dit ding aftasten met de voelspriet $D1$ dan vinden we voor de zin $\tilde{f}$ van $f$: $$ \tilde{f}(x)=\left\{ \begin{array}{ll} 0 & \mbox{voor} \;\; x < -h/2 \\ 1 & \mbox{voor} \;\; x > +h/2 \\ x/h + 1/2 & \mbox{voor} \;\; -h/2 < x < +h/2 \end{array} \right. $$ Nemen we de limiet voor $h \rightarrow 0$, dan wordt de funktie van Heaviside teruggevonden voor $x<0$ en $x>0$, echter niet voor $x=0$. Dit betekent dat $f$ geen zin heeft voor $x=0$, niet precies aangevoeld kan worden in het punt $x=0$. Proberen we in plaats van $D1$ de tastfunktie $D3$ dan vinden we een resultaat dat we hierboven al hadden afgeleid: $ 1/2+1/\pi\,\arctan(x/h)$. Ook deze funktie konvergeert niet naar $1/2$ voor $h \rightarrow 0$. De sprong funktie is ter plaatse $x=0$ onzinnig. Gebruiken we in plaats van $D1$ de Gauss-funktie $D4$, dan komt er: $$ \tilde{f}(x) = \frac{2}{h \sqrt{2 \pi}} \left[ \int_0^x e^{- \frac{1}{2} t^2 / h^2 } \, dt + \frac{1}{2} \right] $$ Afgeleide van de sprong-funktie is de delta-funktie, overigens in de klassiek mathematische opvatting geen echte maar een "oneigenlijke funktie": $$ f(x)=\left\{ \begin{array}{ll} \infty & \mbox{voor} \;\; x = 0 \\ 0 & \mbox{voor} \;\; x \neq 0 \end{array} \right. $$ $$ \mbox{Zodanig dat:} \;\; \int_{- \infty}^{+ \infty} f(x) \, dx = 1 $$ Integratie levert: $$ \tilde{f}(x)=\left\{ \begin{array}{ll} 0 & \mbox{voor} \;\; x < -h/2 \;\; \mbox{en voor} \;\; x > +h/2 \\ 1 / h & \mbox{voor} \;\; -h/2 < x < +h/2 \end{array} \right. $$ Dat is de tastfunktie zelf. Dit is natuurlijk niet toevallig. Gebruiken we in plaats van $D1$ de Gauss-funktie $D4$, dan komt wegens de diafragma-eigenschap ook dezelfde Gauss-funktie weer tevoorschijn.
De vier funkties worden, tezamen met hun (eindige) gevoelswaarden volgens een
normale (Gauss-) verdeling $D4$, weergegeven in de volgende figuur. Details:
$ -1 \leq x \leq +1 $ en $ h = 0.25 $.

Merk op dat het uitsmeer effekt van de tast-funktie des te voelbaarder is naarmate
de gemeten funktie $f$ ter plaatse minder "netjes" is. Het is belangrijk
om dit te onthouden.
Beschouw de Dirichletfunctie : $$ f(x)=\left\{ \begin{array}{ll} 1 & \mbox{voor alle rationale getallen} \\ 0 & \mbox{voor alle irrationale getallen} \end{array} \right. $$ De zin $\tilde{f}$ van deze funktie is te bepalen met behulp van de zogenaamde "maat" theorie van Lebesgue. De uitkomst is: $\tilde{f} = 0 $. Dit betekent dat $f(x)$ geen zin verschillend van nul heeft. We kunnen ook zeggen: op het gevoel is $f(x)$ nul, of de funktie ziet er uit alsof hij helemaal nul is.
Nu is het redelijk te veronderstellen dat het aftasten van een funktie met een ideale voelspriet niets anders naar voren brengt dan de funktie zelf. Er zullen in de materiële werkelijkheid geen funkties zitten "achter" funkties die al op de perfekte manier gemeten zijn, geen realiteit achter een reeds toereikend geïdealiseerde realiteit, geen verdere verborgen parameters, niet nog meer wiskunde achter de wiskunde. In het algemeen behoort dus de zin van een funktie gelijk te zijn aan de funktie zelf: $$ f(x) = \tilde{f}(x) $$ Dit is feitelijk de "diafragma-eigenschap" van de delta-funktie voor "fatsoenlijke" funkties. Het is duidelijk dat alle "nette" funkties ook zinnig zijn. Omgekeerd is een funktie overal "netjes" waar hij zinnig is. Bovenstaande analyse geeft ons een middel in handen om kritiek te hebben op mathematische funkties die niet op zinnige (of zullen we zeggen "zinnelijke") wijze zijn geformuleerd. De funktie van Dirichlet is een voorbeeld van zo'n niet konkreet tastbare, en in deze zin niet alleen plaatselijk, doch geheel en al onzinnige funktie.