Insluitingsmethode voor $\pi$
(1995 versie)
In onderstaande figuur zien we een deel van een cirkel, met daarbinnen (halve)
zijden van twee ingeschreven veelhoeken (: $\overline{TW}$ en $\overline{TS}$)
en daarbuiten (halve) zijden van twee omgeschreven veelhoeken (: $\overline{TP}$
en $\overline{QS}$). De bedoeling is om het aantal zijden van een ingeschreven
of omgeschreven veelhoek iedere keer te verdubbelen, zodat daarmee de cirkel
steeds nauwkeuriger wordt ingesloten. $\overline{TW}$ wordt (de helft van)
$\overline{TS}$ en $\overline{TP}$ wordt $\overline{QS}$:
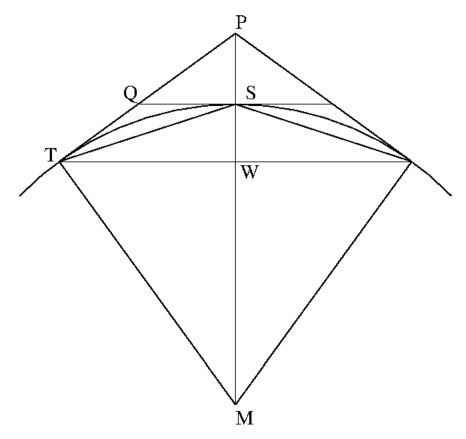
De lengte van een zijde van een ingeschreven veelhoek noemen we $a$, de lengte
van een zijde van een omgeschreven veelhoek noemen we $b$. We geven aan de
eerste benadering een index $n$ en aan de tweede benadering een index $2n$ mee.
Zodoende is:
$$ \overline{TW}=\frac{1}{2} a_n \qquad \overline{TS}=a_{2n} \qquad
\overline{TP}=\frac{1}{2} b_n \qquad \overline{QS}=\frac{1}{2} b_{2n} $$
$R$ is de straal van de cirkel met middelpunt $M$:
$$ \overline{MT}=\overline{MS}=R $$
Verder zijn er een aantal rechte hoeken:
$$ \overline{MP} \perp \overline{TW} \qquad \overline{MP} \perp \overline{QS}
\qquad \overline{MT} \perp \overline{PT} $$
De ingeschreven veelhoeken worden eerst behandeld.
De driehoeken $\bigtriangleup SWT$ en $\bigtriangleup TWM$ zijn rechthoekig.
Twee maal de stelling van Pythagoras toepassend, leiden wij af:
$$
\begin{array}{ll}
\overline{WS}^2+(\frac{1}{2} a_n)^2&=&a_{2n}^2 \\
\overline{MW}^2+(\frac{1}{2} a_n)^2&=&R^2 \\
\overline{MW}+\overline{WS}&=&R
\end{array}
$$
Einde van het meetkundige gedeelte. De rest volgt door middel van pure algebra:
$$ \sqrt{a_{2n}^2-(\frac{1}{2} a_n)^2} + \sqrt{R^2 - (\frac{1}{2} a_n)^2} = R $$
$$ a_{2n}^2-(\frac{1}{2} a_n)^2=R^2+[R^2-(\frac{1}{2} a_n)^2]-2R\sqrt{R^2-(\frac{1}{2} a_n)^2} $$
$$ a_{2n}/R=\sqrt{2-2\sqrt{1-(\frac{1}{2} a_n/R)^2}} $$
In de laatste uitdrukking worden twee bijna even grote getallen afgetrokken van
elkaar. Dit is een gang van zaken die slecht bestand is tegen onnauwkeurigheid.
Oftewel de formule is numeriek instabiel. Het is beter de uitdrukking om
te werken. Dat gaat met behulp van het merkwaardig produkt $(x+y)(x-y)=x^2-y^2$.
Vermenigvuldigen we teller en noemer (gelijk 1) met een faktor van de vorm
$\sqrt{x+y}$, dan komt er: $$ a_{2n}/R =
\frac{\sqrt{4-4[1-(\frac{1}{2} a_n/R)^2]}}{\sqrt{2+2\sqrt{1-(\frac{1}{2} a_n/R)^2}}} =
\frac{a_n/R}{\sqrt{2+2\sqrt{1-(\frac{1}{2} a_n/R)^2}}} $$
Merk op dat in deze formule alleen grootheden voorkomen van de vorm $a/R$.
Het is dus geen beperking van de algemeenheid indien we de straal van de cirkel
normeren op $R=1$:
$$ a_{2n} = \frac{a_n}{\sqrt{2+2\sqrt{1-(\frac{1}{2} a_n)^2}}} \quad \approx \frac{1}{2} a_n
\quad \mbox{voor kleine \ } a $$
Met behulp van bovenstaande figuur leiden wij af voor de omgeschreven veelhoek:
$$ \bigtriangleup MTP \qquad \mbox{rechthoekig} $$
$$ \bigtriangleup MTP \sim \bigtriangleup QSP \quad \Longrightarrow \quad
\frac{\overline{MT}}{\overline{QS}}=\frac{\overline{TP}}{\overline{PS}} $$
Hiermee vinden we twee van de drie vergelijkingen:
$$
\begin{array}{ll}
\overline{MP}^2&=&\overline{MT}^2+\overline{TP}^2=R^2+(\frac{1}{2} b_n)^2 \\
\Large \frac{R}{\frac{1}{2} b_{2n}} &=& \Large \frac{\frac{1}{2} b_n}{\overline{SP}} \\
\overline{SP}&=&\overline{MP}-R
\end{array}
$$
Algebraisch verwerken levert:
$$ \frac{R}{\frac{1}{2} b_{2n}}=\frac{\frac{1}{2} b_n}
{\sqrt{(\frac{1}{2} b_n)^2+R^2}-R} \quad \Longrightarrow \quad
b_{2n}/R=\frac{\sqrt{(\frac{1}{2} b_n/R)^2+1}-1}{\frac{1}{2} \frac{1}{2} b_n/R} $$
Ook deze formule is numeriek instabiel. Vermenigvuldig teller en noemer weer
met een faktor, van de vorm $(x+y)$, dan komt er: $$ b_{2n}/R =
\frac{4 \left[ (\frac{1}{2} b_n/R)^2+1-1 \right]}
{b_n/R\left[\sqrt{(\frac{1}{2} b_n/R)^2+1}+1\right]}
= \frac{b_n/R}{1+\sqrt{1+(\frac{1}{2} b_n/R)^2}} $$
Substitueer ook hier $b:=b/R$, dan is tenslotte:
$$ b_{2n} = \frac{b_n}{1+\sqrt{1+(\frac{1}{2} b_n)^2}} \quad \approx \frac{1}{2} b_n
\quad \mbox{asymptotisch} $$
Als beginwaarde voor de ingeschreven veelhoeken kan men nemen de ingeschreven
zeshoek. Dit is gemakkelijk: die heeft een zijde van 1. Drie maal deze lengte
is een onderkant benadering voor $\pi$. Als beginwaarde voor de omgeschreven
veelhoeken kan men nemen de omgeschreven vierhoek. Deze heeft een zijde van 2.
Twee maal deze lengte is een bovenkant benadering voor $\pi$. We gaan nu van
beide veelhoeken iedere keer het aantal zijden verdubbelen. De hele procedure
kan gemakkelijk konkreet worden gemaakt in een BASIC programmaatje dat, na het
uitgebreide betoog van hierboven, verrassend kort uitpakt:
10 REM ** Insluitingsmethode om \pi te bepalen **
20 A=1 : B=2 : N=1 : REM Beginwaarden
30 A=A/SQR(2+2*SQR(1-(A/2)^2)) : REM Ingeschreven
40 B=B/(1+SQR(1+(B/2)^2)) : REM Omgeschreven
50 N=N*2 : PRINT 3*N*A;2*N*B : REM gaat naar \pi
60 INPUT K : GOTO 30 : END
Nadelig aan de methode is dat het interval voor $\pi$ voortdurend wordt begrensd
door irrationale in plaats van rationale getallen. Meetkundig elegant maar
rekenkundig een ramp. Bovendien blijkt uit de asymptotische benaderingen dat de
convergentie slechts lineair is: iedere keer wordt één "binaaltje" bijgemaakt.
